浅谈数据挖掘中的数据处理（缺失值处理以及异常值检测）

一直想把数据预处理的逻辑给理清楚点，在这里和大家一起分享。

一：缺失值的处理

1. 删除缺失值

这是一种很常用的策略。

缺点：如果缺失值太多，最终删除到没有什么数据了。那就不好办了。

2.2 缺失值的填补

    （1）均值法

        根据缺失值的属性相关系数最大的那个属性把数据分成几个组，然后分别计算每个组的均值，把这些均值放入到缺失的数值里面就可以了。

缺点：改变了数据的分布，还有就是有的优化问题会对方差优化，这样会让对方差优化问题变得不准确。

    （2）随机填补

        一直感觉这个方法不好，就是随机在那一列属性中找个数填补到缺失值里。

    缺点：不靠谱。

    （3）热卡填补法

    对于一个包含缺失值的变量，热卡填充法的做法是：在数据库中找到一个与它最相似的对象，然后用这个相似对象的值来进行填充。不同的问题可能会选用不同的标准来对相似进行判定。最常见的是使用相关系数矩阵来确定哪个变量（如变量Y）与缺失值所在变量（如变量X）最相关。然后把所有变量按Y的取值大小进行排序。那么变量X的缺失值就可以用排在缺失值前的那个个案的数据来代替了。

缺点：太麻烦。与均值替换法相比，利用热卡填充法插补数据后，其变量的标准差与插补前比较接近。但在回归方程中，使用热卡填充法容易使得回归方程的误差增大，参数估计变得不稳定，而且这种方法使用不便，比较耗时。

（4）最近距离决定填补法

假设现在为时间y,前一段时间为时间x，然后根据x的值去把y的值填补好。

缺点：一般就是在时间因素决定不显著的时候，比如一天的气温，一般不会突然降到很低，然后第二天就升的很高。但是对时间影响比较大的，可能就不可以了。

（5）回归填补法

假设我y属相缺失，然后我知道x属性，然后我用回归方法对没有确实的数据进行训练模型，再把这个值得x属性带进去，对这个y属性进行预测，然后填补到缺失处。

缺点：由于是根绝x属性预测y属性，这样会让属性之间的相关性变大。这可能会影响最终模型的训练。

（6）多重填补方法（M-试探法）

它是基于贝叶斯理论的基础上，然后用EM算法来实现对缺失值进行处理的算法。对每一个缺失值都给M个缺失值，这样数据集就会变成M个，然后用相同的方法对这M个样本集进行处理，得到M个处理结果，总和这M个结果，最终得到对目标变量的估计。其实这个方法很简单，就是我尽量多做模型，然后找出最好的，我就叫它M-试探法吧

2.3 基于距离的填补方法

1 k-最近邻法

先根绝欧氏距离和马氏距离函数来确定具有缺失值数据最近的k个元祖，然后将这个k个值加权（权重一般是距离的比值吧）平均来估计缺失值。

1. 有序最近邻法

这个方法是在K-最近邻法的基础上，根据属性的缺失率进行排序，从缺失率最小的进行填补。这样做的好处是讲算法处理后的数据也加入到对新的缺失值的计算中，这样即使丢了很多数据，依然会有很好的效果。在这里需要注意的是，欧式距离不考虑各个变量之间的相关性，这样可能会使缺失值的估计不是最佳的情况，所以一般都是用马氏距离进行最近邻法的计算。

2.4 基于贝叶斯的方法

就是分别将缺失的属性作为预测项，然后根据最简单的贝叶斯方法，对这个预测项进行预测。但是这个方法有一个缺点，就是说不能把之前的预测出来的数据加入到样本集，会丢失一些数据，会影响到预测。所以现在就是对属性值进行重要性排序，然后把重要的先预测出来，在加入新的数据集，再用新的数据集预测第二个重要的属性，这样一直处理到最后为止。

二：平滑噪声数据

暂略（等我下篇文章在总结）

三：探测异常值

首先来说说什么叫异常值。

定义：由于系统误差，人为误差或者固有数据的变异使得他们与总体的行为特征，结构或相关性等不一样，这部分数据称为异常值。

再来说说异常值检测的作用。

应用：异常值检测在数据挖掘中有着重要的意义，比如如果异常值是由于数据本身的变异造成的，那么对他们进行分析，就可以发现隐藏的更深层次的，潜在的，有价值的信息。例如发现金融和保险的欺诈行为，黑客入侵行为，还有就是追寻极低或者极高消费人群的消费行为，然后做出相对应的产品。

那我们如何把异常值检查出来呢？

异常值检测的方法：

3.1 统计学方法对异常值的检测

（1）3σ探测方法

3σ探测方法的思想其实就是来源于切比雪夫不等式。

对于任意ε>0，有：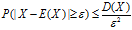

当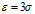时，如果总体为一般总体的时候，统计数据与平均值的离散程度可以由其标准差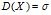反映，因此有：。

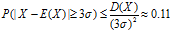一般所有数据中，至少有3/4（或75%）的数据位于平均数2个标准差范围内。

所有数据中，至少有8/9（或88.9%）的数据位于平均数3个标准差范围内。

所有数据中，至少有24/25（或96%)的数据位于平均数5个标准差范围内。

所以如果我们一般是把超过三个离散值的数据称之为异常值。这个方法在实际应用中很方便的使用，但是他只有在单个属性的情况下才适用。

（2）散点图

其实就是画图。把所有点都画出来。自然异常点就出来了。形如这样：

是不是这样异常点一下就看出来了？当然这不就是聚类吗。。。聚类我们之后在说，不急，哈哈。

（3）四分位数展布法

首先，我们介绍什么叫四分位数。如下图所示：

把数据按照从小到大排序，其中25%为上四分位用FL表示，75%处为下四分位用FU表示。

计算展布为：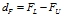

上截断为：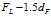

下截断点为：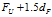

上面的参数1.5不是绝对的，而是根据经验，但是效果很好哦。我们把异常值定义为小于上截断点，或者大于下截断点的数据称为异常值。

优点：与方差和极差相比，更加不如意受极端值的影响，且处理大规模数据效果很好。

缺点：小规模处理略显粗糙。而且只适合单个属相的检测。

（4）基于分布的异常值检测

本方法是根据统计模型或者数据分布。然后根绝这些模型对样本集中的每个点进行不一致检验的方法。

不一致检验：零假设和备选假设。表示我的数据分布或者概率模型满足H1，但是如果我这个值接受另外的数据模型或者概率分布H2。那么我们就认为这个数据点与总体分布不符合，是一个异常值。

下面介绍几种方法：

1：Grubbs检验

步骤一：先把数据按照从小到大的顺序排列x₁,x₂…x_n。

步骤二：假设我们认为x_i为异常点。计算平均值。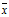

步骤三：计算算数平均值和标准差的估计量s。

            公式为：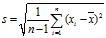

步骤四：计算统计量g_i

        计算公式为：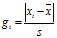

步骤五：将g_i与查Grubbs检验法的临界值表所得的g(a,n)进行比较。如果gi< g(a,n),那么则认为不存在异常值，如果大于，就认为这个点是异常值。

这样异常值被选出来后，重复以上步骤，直到没有异常值为止。

2：Dixon检测方法

步骤一：先把数据按照从小到大的顺序排列x1,x2…xn。

步骤二：当3时候，r_大=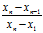，r_小=，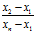

        当8时候，r_大=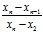，r_小=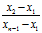

        当n时候，r_大=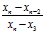，r_小=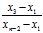

步骤三：将r_大，r_小分别与Dixon检验法的临界值表得到的临界值r(a,n)进行比较、如果r_大（r_小）>r(a,n),可以认为最大（最小）的值为异常值，否则就不是异常值。

3t分布检验方法

将怀疑是异常值的数据选出来，然后根据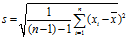，然后查t分布临界值得到临界值t(a,n-1)。如果被挑出的数据确实为异常值的话应该满足下式子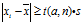：。这样异常值就确认了。

上面的一些方法只适用于单维数据。而且还必须确定其数据分布，所以不是太准确。

3.2 基于距离的异常值检测

基于距离的定义：在样本集S中，O是一个异常值，仅当 S中有p部分的距离大于d。可以这样理解：

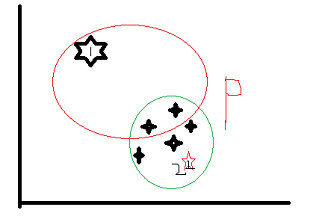
图中与五角星1距离超过d的有三个点。。。我们就可以说他是异常点，假如阀值是2，现在2五角星的距离超过d的只有五角星一个。所以五角星2不是异常点。当然这个距离的计算还是用到马氏距离。

优缺点：可以多维数据监测，无需估计样本的分布，但是受参数影响严重。

3.3 基于偏离的异常值检测

假设N的数据集，建立数据子集。求出子集间得相异度，然后确定异常值。

较为复杂，计算量大。不建议使用.

3.4 基于分类模型的异常值检测

根据已有的数据，然后建立模型，得到正常的模型的特征库，然后对新来的数据点进行判断。从而认定其是否与整体偏离，如果偏离，那么这个就是异常值。

1. 建立贝叶斯模型
2. 神经网络模型
3. 分类模型
4. 决策类分类
5. SVM的方法

其实这些和以前介绍的基本方法差不多。

总结：数据预处理是数据挖掘前期最重要的部分，本文对缺失数据及异常值检测进行了总结，具体实现，还得看你在什么样的平台上实现。这里只是提供逻辑上的思考。本花一直认为逻辑正确才能下手做事！。。。逻辑混乱，那么大脑就一直是混沌状态。。。

祝大家元旦快乐！