笨笨熊搬家打包篇

描述:

  
森林里的笨笨熊今天可开心啦——他买了新房子，乔迁新喜要搬家了。因此，笨笨熊请了许多好朋友来帮忙搬家，并准备了很多小纸盒用来装需要搬的物品，不过，这些纸盒的容积都是相同的，并且最多只能装两个物品。但是，为了不打扰太多的朋友，笨笨熊想了个“聪明”办法：让每个纸盒使用效率最高(注：只要纸盒容积大于物品的体积之和就认为可以装下；物品体积不会大于纸盒容积)，这样需要的纸盒最少。为了帮助笨笨熊提前通知朋友，请你根据笨笨熊的办法，帮忙算出：需要纸盒的最少数目是多少？        
运行时间限制: 无限制 内存限制: 无限制 输入:  
整数V——纸盒的容积； 整数N——物品的总数目N； 
共N个整数(对应N个物品的体积,每个整数用空格隔开)。   
输出:  
整数M——需要纸盒的最少数目

样例输入：
10
2
2 3
样例输出：
1

 这里给出一种比较容易实现的解法：首先对所有物品的体积按从小到大进行排序，然后设计两个指针分别指向目前“未装箱”的容积最小和最大的物品，然后首先判断容积最大的物品是否小于盒子的容积，如果是，则判断加上最左边容积最小的物品后体积是否仍然小于盒子容积，如果仍然小，则left指针向右移动一个位置，继续判断，直到总和超过盒子容积停止，并将计数器加1，进入下一轮判断。

#include <stdio.h>
#include <stdlib.h>

//插入排序
void insertion_sort(int a[], int n)
{
    int i, j, t;

    for (i = 0; i < n-1; i++){
        for (j = i+1; j > 0; j--){
            if (a[j] < a[j-1]){
                t = a[j];
                a[j] = a[j-1];
                a[j-1] = t;
            }else break;
        }
    }
}

//先排序,然后最大与最小相加
int box_count(int volume[], int n, int box_size)
{
    int left = 0, right = n-1, count = 0, total;

    insertion_sort(volume, n);

    while (left <= right){
        if (volume[right] <= box_size){
            total = volume[right];
            while (left < right && total + volume[left] <= box_size){
                total += volume[left];
                left++;
            }
            count++;
            right--;
        }
    }

    return count;
}

int main(void)
{
    int i, box_size, num;
    int *list;

    scanf("%d", &box_size);//纸箱容积
    scanf("%d", &num);     //物品个数

    list = (int *)malloc(num * sizeof(int));
    //依次输入每个物品的体积
    for (i = 0; i < num; i++){
        scanf("%d", &list[i]);
    }

    printf("%d
", box_count(list, num, box_size));

    return 0;
}

 但是，这种方法可能存在一些问题，因为到最后小的物品都装完了，可能导致剩下的每一件物品都需要占用一个盒子的情况。为此，我们切换一种思路：仍然首先对这些物品按照体积从小到大进行排序，然后从最大的物品开始查找，如果体积最大的物品未装箱（需要使用额外的空间来存储该物品是否已经装箱），就首先将其装入箱中，然后从体积次大的物品开始搜索，如果该物品未装箱并且能够继续装入箱中，则添加到此箱中，如果不过，再检查更小的物品，直到遍历至体积最小物品停止。

//先排序，然后最大加上次大，依次寻找满足条件的组合
int box_count2(int volume[], int n, int box_size)
{
    int left = 0, right = n-1, count = 0, total;
    int* flag = (int *)calloc(n, sizeof(int));//用于标记对应元素是否已经装箱

    insertion_sort(volume, n);

    printf("Method 2#
");
    while (right >= 0){//从最大向最小寻找
        if (flag[right] == 0 && volume[right] <= box_size){
            printf("[ %d ", volume[right]);//输出满足条件的组合

            flag[right] = 1;//将此物品装箱
            total = volume[right];
            left  = right - 1;
            while (left >= 0){
                //如果左侧物品未装箱并且可以继续加入本箱中
                if (flag[left] == 0 && total + volume[left] <= box_size){
                    printf("%d ", volume[left]);//输出满足条件的组合

                    flag[left] = 1;//将此物品装箱
                    total += volume[left];
                }
                left--;
            }

            //装满一箱
            printf("]
");
            count++;
        }
        right--;
    }

    return count;
}

然后，我们可以重新写一个测试程序，输出两种方法的装箱结果，完整代码如下：

#include <stdio.h>
#include <stdlib.h>

//插入排序
void insertion_sort(int a[], int n)
{
    int i, j, t;

    for (i = 0; i < n-1; i++){
        for (j = i+1; j > 0; j--){
            if (a[j] < a[j-1]){
                t = a[j];
                a[j] = a[j-1];
                a[j-1] = t;
            }else break;
        }
    }
}

//先排序,然后最大与最小相加
int box_count(int volume[], int n, int box_size)
{
    int left = 0, right = n-1, count = 0, total;

    insertion_sort(volume, n);

    printf("Method 1#
");
    while (left <= right){
        if (volume[right] <= box_size){
            printf("[ %d ", volume[right]);//输出满足条件的组合
            total = volume[right];
            while (left < right && total + volume[left] <= box_size){
                printf("%d ", volume[left]);
                total += volume[left];
                left++;
            }
            printf("]
");
            count++;
            right--;
        }
    }

    return count;
}

//先排序，然后最大加上次大，依次寻找满足条件的组合
int box_count2(int volume[], int n, int box_size)
{
    int left = 0, right = n-1, count = 0, total;
    int* flag = (int *)calloc(n, sizeof(int));//用于标记对应元素是否已经装箱

    insertion_sort(volume, n);

    printf("Method 2#
");
    while (right >= 0){//从最大向最小寻找
        if (flag[right] == 0 && volume[right] <= box_size){
            printf("[ %d ", volume[right]);//输出满足条件的组合

            flag[right] = 1;//将此物品装箱
            total = volume[right];
            left  = right - 1;
            while (left >= 0){
                //如果左侧物品未装箱并且可以继续加入本箱中
                if (flag[left] == 0 && total + volume[left] <= box_size){
                    printf("%d  ", volume[left]);//输出满足条件的组合

                    flag[left] = 1;//将此物品装箱
                    total += volume[left];
                }
                left--;
            }

            //装满一箱
            printf("]
");
            count++;
        }
        right--;
    }

    return count;
}


int main(void)
{
    int i, box_size, num;
    int *list;

    scanf("%d", &box_size);//纸箱容积
    scanf("%d", &num);     //物品个数

    list = (int *)malloc(num * sizeof(int));
    //依次输入每个物品的体积
    for (i = 0; i < num; i++){
        scanf("%d", &list[i]);
    }

    printf("%d
", box_count(list, num, box_size));
    printf("%d
", box_count2(list, num, box_size));

    printf("Done.
");
    return 0;
}

为了测试这两种算法的差异，我们输入的物品体积尽量比箱子容量的一半大一点，本次测试用的数据如下：

运行程序，输出结果如下：

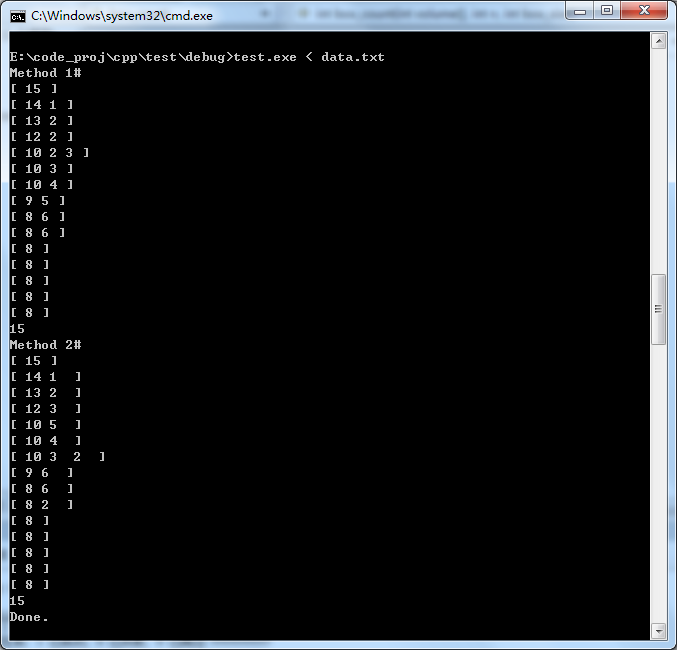
从这个测试结果来看，两种算法输出的箱子总数还是相同的，只不过组合不同，第二种方法能够按照total从大到小的顺序输出结果，而第一种方法没有规律可言。

有没有人能够找出一组数据使得两种方法输出结果不同呢？