“树状数组的题线段树都能做。那我们为什么要学习树状数组,直接用线段树搞不就好了。zz,既然用短小而精悍的树状数组能搞,还用100多行的线段树?”
以上为qbxt某位神牛一人饰两角倾情演绎。
蒟蒻在临近noip之时终于搞懂了树状数组,在此做一下总结,算是巩固?
类似线段树,我们可以分三种模板
1、单点修改,区间求和
2、区间修改,单点查询
3、区间修改,区间求和
朴素算法是直接在数组上更改,1的复杂度是O(n+m*l),2复杂度是O(n*l+m),3的复杂度是O(n*l+m*l)(n为修改次数,m为查询次数,l为数组长度),复杂度是非常高的,范围稍微大一点就无法承受了,这时候就可以想到树状数组了,树状数组的复杂度是(m+n)*logl的,复杂度中的log是怎么来的呢....
说到树状数组,下面这个图是必不可少的(图是我盗的....)
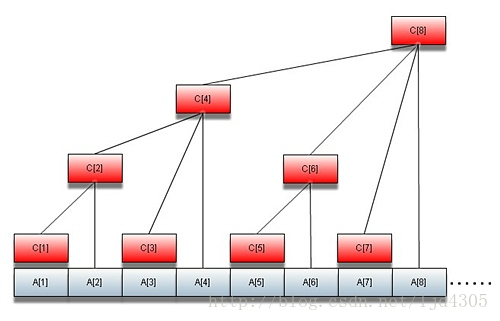
这个c数组就是树状数组,观察一下可以发现:
c[1]=a[1],
c[2]=a[1]+a[2]=c[1]+a[2],
c[3]=a[3],
c[4]=a[1]+a[2]+a[3]+a[4]=c[2]+c[3]+a[4],
c[5]=a[5],
c[6]=a[5]+a[6],
c[7]=a[7],
c[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8],
有什么规律,c数组又a数组的那几个组成,把c数组下标转为二进制:
1-->00000001
2-->00000010
3-->00000011
4-->00000100
5-->00000101
6-->00000110
7-->00000111
8-->00001000
假设c[i]中的i的二进制中末尾0的个数为x(比如说:6,6的二进制中末尾有1个0,x=1),c[i]=a[i]+a[i-1]+…+a[i-2^x+1](c[6]=a[6]+a[5]),这时我们就要用到一个很重要的函数,lowbit(int x)用来求2^x,,这2^x个元素是从后往前递减的
int lowbit(int x) { return x&(-x); }
修改单点的元素时,只需要把该元素到根节点的路径上的c[]改变就行了,查询时也只需要从该路径上查找,由于树的深度最多为logl(可以看成二叉树),那么复杂度就会降下很多,这就是开头我们提到的log来源了
修改c[i]也要将i所在路径上的c[]全部修改,也就是持续向上找father,i的父亲节点为i+lowbit(i),
void add(int i,int val) { if(i==0) return;//这步去掉似乎也可以 while(i<=n) { c[i]+=val; i+=lowbit(i); } }
求区间[a,b]的和,ans=sum(b)-sum(a-1),sum为从1到该点的a[]和
int sum(int i) { int s=0; while(i>0) { s+=c[i]; i-=lowbit(i); } return s; }
第一种情况就是这样了,第二三种情况区间修改我们可以利用查分的思想,其他的都差不多........吧

1 //1、单点修改,区间查询 2 #include<cstdio> 3 #include<cstring> 4 #include<iostream> 5 using namespace std; 6 int c[500010]; 7 int n,m; 8 int lowbit(int x) 9 { 10 return x&(-x); 11 } 12 void add(int i,int val) 13 { 14 if(i==0) return ; 15 while(i<=n) 16 { 17 c[i]+=val; 18 i+=lowbit(i); 19 } 20 } 21 int sum(int i) 22 { 23 int s=0; 24 while(i>0) 25 { 26 s+=c[i]; 27 i-=lowbit(i); 28 } 29 return s; 30 } 31 int main() 32 { 33 int v; 34 scanf("%d%d",&n,&m); 35 for(int i=1;i<=n;i++) 36 scanf("%d",&v), 37 add(i,v); 38 for(int i=1;i<=m;i++) 39 { 40 int x,y,z; 41 scanf("%d%d%d",&x,&y,&z); 42 if(x==1) add(y,z); 43 if(x==2) printf("%d ",sum(z)-sum(y-1)); 44 } 45 return 0; 46 }

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 using namespace std; 5 int c[500010]; 6 int n,m; 7 int lowbit(int x) 8 { 9 return x&(-x); 10 } 11 void add(int i,int val) 12 { 13 if(i==0) return ; 14 while(i<=n) 15 { 16 c[i]+=val; 17 i+=lowbit(i); 18 } 19 } 20 int sum(int i) 21 { 22 int s=0; 23 while(i>0) 24 { 25 s+=c[i]; 26 i-=lowbit(i); 27 } 28 return s; 29 } 30 int main() 31 { 32 scanf("%d%d",&n,&m); 33 for(int i=1;i<=n;i++) 34 { 35 int v; 36 scanf("%d",&v); 37 add(i,v); 38 add(i+1,-v); 39 } 40 for(int i=1;i<=m;i++) 41 { 42 int p,x,y,z; 43 scanf("%d",&p); 44 if(p==1) 45 { 46 scanf("%d%d%d",&x,&y,&z); 47 add(x,z); 48 add(y+1,-z); 49 } 50 if(p==2) 51 { 52 scanf("%d",&x); 53 printf("%d ",sum(x)); 54 } 55 } 56 return 0; 57 }
