排序
一、 基本概念
排序(sorting)的功能是将一个数据元素的任意序列,重新排列成一个按关键字有序的序列。
内部排序与外部排序
根据排序时待排序的数据元素数量的不同,使得排序过程中涉及的存储器不同,可以将排序方法分为两类。一类是整个排序过程在内存储器中进行,称为内部排序;另一类是由于待排序元素数量太大,以至于内存储器无法容纳全部数据,排序需要借助外部存储设备才能完成,这类排序称为外部排序。
稳定与不稳定
如果在待排序的序列中存在多个具有相同关键字的元素。假设Ki=Kj(1≤ i≤ n,1≤ j≤n,i≠j),若在排序之前的序列中Ri在Rj之前,经过排序后得到的序列中Ri仍然在Rj之前,则称所用的排序方法是稳定的;否则,当相同关键字元素的前后关系在排序中发生变化,则称所用的排序方法是不稳定的。
例子:学生纪录学号小的学生在前,现在需要根据学生的成绩排序,当分数相同时要求学号小的学生在前,显然此时对分数进行排序就必须选择稳定的排序方法。
二、 排序方法分类
内部排序的方法很多,但是很难说哪一种内部排序方法最好,每一种方法都有各自的优缺点,适合于不同的环境下使用。如果按照排序过程中依据的原则对内部排序进行分类,则大致上可以分为插入排序、交换排序、选择排序、归并排序等排序方法。
插入排序:
插入排序的基本排序思想是:逐个考察每个待排序元素,将每一个新元素插入到前面已经排好序的序列中适当的位置上,使得新序列仍然是一个有序序列。在这一类排序中主要有三种排序方法:直接插入排序、折半插入排序和希尔排序。
交换排序:
交换类排序主要是通过两两比较待排元素的关键字,若发现与排序要求相逆,则“交换”之。在这类排序方法中最常见的是冒泡排序和快速排序,其中快速排序是一种在实际应用中具有很好表现的算法。
选择排序:
选择排序的基本思想是:每一趟从n-i+1 (i=1,2,…,n)个元素中选取一个关键字最小的元素作为有序序列中第i个元素。最常见的是简单选择排序,树型选择排序,堆排序。
归并排序:
归并排序是另一类不同的排序方法,这种方法是运用分治法解决问题的典型范例。归并排序的基本思想是基于合并操作,即合并两个已经有序的序列是容易的,不论这两个序列是顺序存储还是链式存储,合并操作都可以在Ο(m+n)时间内完成(假设两个有序表的长度分别为m 和n)。
三、 基于比较的排序方法对比
上面介绍的插入排序、交换排序、选择排序、归并排序等排序方法,都有一个共同的特点,那就是它们都是通过比较元素的大小来确定元素之间的相对位置的,即上述排序方法都是基于比较的排序方法。基于比较的排序方法进行一个对比如下:
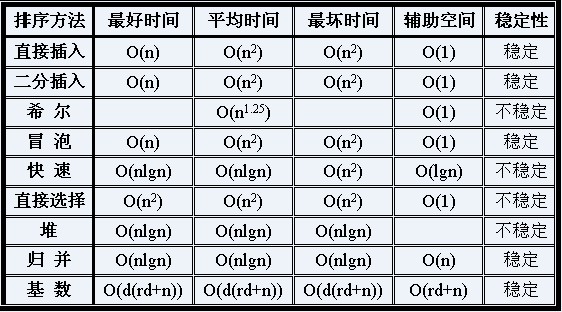
四、 基于比较的排序时间复杂度下限
问题:基于比较的排序方法,其可能达到的最快速度是什么,即排序方法的时间复杂度下界?
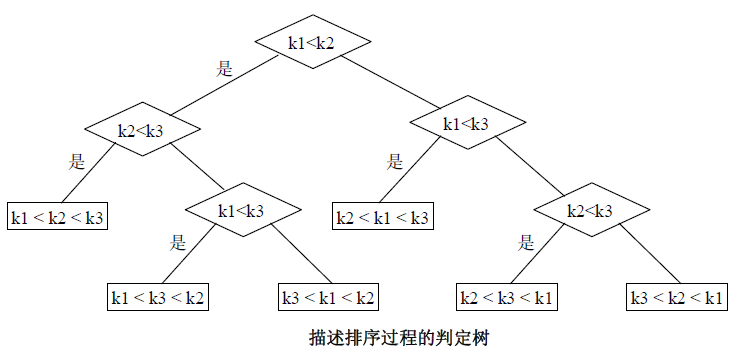
图中所示的判定树表示3个关键字分别为k1、k2 和k3 的元素进行直接插入排序的过程,树中每个非终端结点表示两个元素间的一次比较,其左右子树分别表示这次比较的结果。假设k1≠k2≠k3,则3个元素之间只可能有如下6种大小关系:(1)k1<k2<k3;(2)k1<k3<k2;(3)k2<k1<k3;(4)k2<k3<k1;(5)k3<k1<k2;(6) k3<k2< 1,也就是说,在经过排序之后只可能得到以下6种结果:(1){k1, k2, k3};(2){ k1, k3, k2};(3){ k2, k1, k3};(4){k2, k3, k1};(5){ k3, k1, k2};(6){ k3, k2, k1},而图中判定树的6 个叶子结点恰好表示了这6种排序结果。判定树上进行的每一次比较都是必要的,因此,这个判定树足以描述基于比较操作的排序过程。并且,对于每个初始序列经过排序达到有序所需比较的次数,恰为从根结点到和该序列对应的叶子结点的路径长度。由图可以看出,对3个关键字进行排序,则至少需要进行3次比较。
推广至一般的情况,对n个元素进行排序至少需要多少次比较,由于n个元素的序列可能出现的排序结果有n!个,则描述n个元素排序过程的判定树必有n!个叶子结点。这个问题等价于:含有n!个叶子结点的二叉树的最小高度是多少。
引理 设T 是一棵有n!个叶子结点的二叉树,则T 的高度至少是Ω(nlong n)。
证明:设m是T中叶子结点数,并设h是它的高度。通过观察知道,当所有叶子结点出现在h层时,叶子结点达到最大值,此时,h层上结点最多可以有2h个。因为m=n!,我们有n! = m ≤2h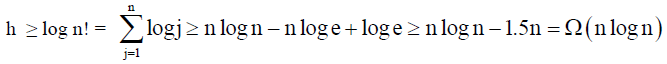
任何一个基于比较操作的排序方法,在最坏情况下所需要进行的比较次数至少为nlogn 次,即算法的时间复杂度下界为Ω(nlog n)。