线性回归的代码。具体要求如下:
(1)回归函数为:x^2-0.5 + noisy
(2)神经网络的层数、节点数目、激活函数自定义。(记录心得)
(3)使用tensorboard把计算图显示出来。
(4)使用matplotlib.pyplot把拟合情况画出来。
一、初始数据如下:
线性回归函数:x^2-0.5 + noisy
step_num = 400
lr = 0.01
batch_size = 10
二、参数调优过程数据如下:
1、调参数据:step_num = 400,lr = 0.01,batch_size = 10得到的, 得到损失
函数为0.0122,图像显示极度欠拟合。
2、增加神经元层数:把神经元层数从1层改为4层,发现拟合程度变化不明显。
3、增加step_num,值为5000时,曲线拟合效果有明显改变,但底部不光滑,有折
线。
4、增加Batch_size至50,有细微的改变,但是改变不是很明显。
5、改变激活函数,尝试Tanh、relu、sigmoid等,感觉Tanh函数效果较好
6、增加step_num至12000,效果显著,损失函数达到最小值0.0043,曲线基本拟合。
7、改变学习率,效果不是很明显。
8、将激活函数全部改为Tanh,曲线拟合较好,减少神经元层数至1层,曲线拟合也比
较好,损失函数为0.0033
9、将优化函数从GradientDescentOptimizer改为AdamOptimizer,拟合效果很好,
将step_num改为12000-18000,效果非常好,多跑几次损失函数最小值可以达到
0.0024,曲线已经非常拟合了。
三、生成的图如下:
1、运行代码通过matplolib画出来的图如下:

四、获取计算图如下:
1、在terminal终端输入如下内容:
D: ensorflow> tensorboard logdir D:AIwork1.py
2、在谷歌浏览器输入:http://127.0.0.1:6006
3、显示如下图:
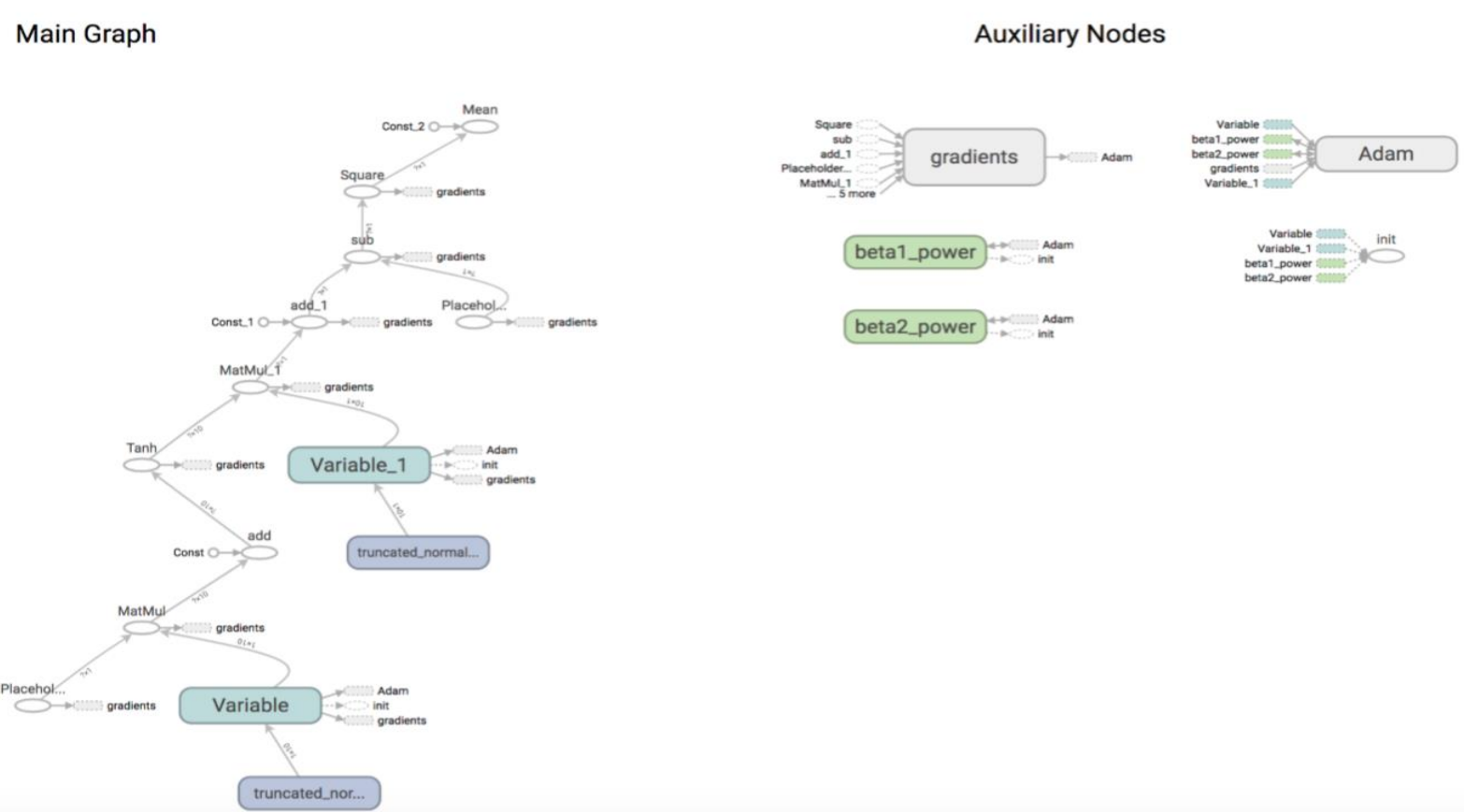
五、结论
1、把激活函数从relu和sigmoid改为tanh最符合此次模型的拟合
2、发现在参数调优过程当中起重大作用的还是选择了AdamOptimizer这个优化器,
可以快速均匀的进行收敛。
3、增加神经元的层数对此次的数据拟合效果不是特别明显。
4、batch_size的值改到500-800的时候损失函数的会下降会更加的稳定,不会剧烈的
来回震荡,但对最终的拟合作用不是很大。
4、在此次调优过程中step_num从12000往上增加步数,拟合的效果会越来越好,直
到18000损失函数达到 0.0024左右,明显感觉到下降的梯度会越来越慢,所以
step_num参数对线性回归的调优其实作用还是很大的。

