3.1概述
3.1.1线性
如果L是加性的且是单一性的(即满足叠加原理),则称该映射是线性的。等价的,对于任意的矢量x,y和标量a,b,线性映射满足L(ax+by)=aLx+bLy,即它保持线性组合。
3.1.2狄拉克分布和卷积
理想的冲击是一个重要的输入信号,图像平面上的理想冲击使用狄拉克分布定义的,δ(x,y)
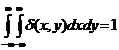
且对于所有的x,y≠0,有δ(x,y)=0.
狄拉克分布的“筛特性”: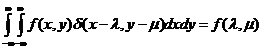 它提供了函数f(x,y)在点λ,μ的值:
它提供了函数f(x,y)在点λ,μ的值:
卷积是一个积分,反映一个函数f(t)在另一个函数上h(t)移动时所叠加的量。函数f和h的在有限域[0,t]上的1D卷积f*h由下式给出:
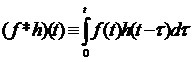
卷积具有如下性质:
f*h=h*f
f*(g*h)=(f*g)*h
f*(g+h)=(f*g)+(f*h)
a(f*g)=(af)*g=f*(ag)
对卷积做微分: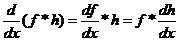
离散卷积用求和来表达: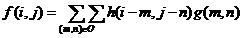 ,称h 为卷积掩膜,一般使用奇数的行和列的矩形邻域O,这样能够确定邻域的中心。
,称h 为卷积掩膜,一般使用奇数的行和列的矩形邻域O,这样能够确定邻域的中心。
3.2积分线性变换
在图像分析中最常用的积分线性变换是傅里叶变换、余弦变换和小波变换。在图像处理中积分线性变换通常的应用是图像滤波,滤波既可在空域也可在频域进行。在频域,滤波可看作增强或减弱特定频率。
3.2.1作为线性系统的图像
由图像及其处理可以建模为由狄拉克冲击δ表达一个的点展开函数的叠加。算子是从一个矢量空间到另一个矢量空间的映射。一个线性算子L(也称作线性系统)具有如下性质:L{af1+bf2}=aL{f1}+bL{f2}
一幅图像f可以表示成由狄拉克冲击δ表达的点展开函数的线性组合。线性系统L对输入图像f的响应g由下式给出:
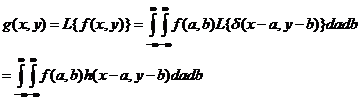
其中h是线性系统L的冲击响应。即线性系统L的输出可以表示为输入图像f与该线性系统的冲击响应h的卷积。对其两边作傅里叶变换,则G(x,y)=F(u,v)*H(u,v)
该式常用于图像预处理中表示平滑和锐化的处理。在实际中,很多情况下图像可以用线性系统来近似。
3.2.2 1D傅里叶变换
1D傅里叶变换F将一个函数f(t)变换到频域表达F{f(t)}=F(ξ),其中ξ[Hz=s-1]是频率而2πξ[s-1]是角频率。复函数F称作(复)频谱。
设i是通常的虚数单位。连续傅里叶变换F由下式给出:
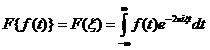
傅里叶逆变换F-1为

函数f(t)的傅里叶谱存在的条件是:
(1)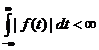 ,即f必须比指数函数衰减更快。
,即f必须比指数函数衰减更快。
(2)f在任有限何有限的区间内只能有有限个不连续点。
注:任何1D函数f(t)的形状都可以分解为它的偶对称fe(t)和奇对称fo(t)部分。fe(t)=(f(t)+f(-t))/2,fo(t)=(f(t)-f(-t))/2
帕斯维尔定理: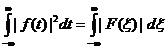
测不准原理指出:不可能存在时域和频域都可以任意窄的信号。
离散傅里叶变换定义为:
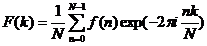
其逆变换定义为:
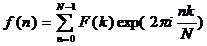
谱F(k)是周期性的,周期是N。
3.2.4 2D傅里叶变换
连续图像函数f的2D傅里叶变换定义为如下的积分:

其傅里叶逆变换为:
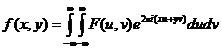
参数(x,y)表示图像坐标,(u,v)称为空间频率。
2D傅里叶变换的结果是一个复值的2D谱。
3.2.4 采样与香农约束
一个连续的图像函数f(x,y)可以用平面上离散的栅格点来采样。
香农采样定理: ,在图像分析中该定理的一个简单的物理解释是:设已知图像中感兴趣的最小细节的尺寸,采样间隔应该比它的一半要小。
,在图像分析中该定理的一个简单的物理解释是:设已知图像中感兴趣的最小细节的尺寸,采样间隔应该比它的一半要小。
3.2.5离散余弦变换(DCT)
DCT作用域有限长度的函数样本上,对于有限长度的离散序列有两个选项与边界条件有关。其一是函数是否在定义域左端和右端都是偶或奇的,其二是相对于哪点函数是偶或奇的。
3.2.6小波变换
定位信号(图像)中的变化的一种解决办法是使用短时傅里叶变换,其中信号被分解为小窗口并将其看作周期函数作局部处理。
小波变换比短时傅里叶变换更进一步。它分析信号(图像)也是通过乘以窗函数并作正交展开来进行,与其他积分线性变换类似。小波分析在两个方向上做了扩展。在第一个方向上,基函数(称作小波(wavelet)意指很小的波,或母小波)比正弦和余弦要复杂。5种常用的母小波的形状为:

在第二个方向上,小波分析是在多个尺度上进行的。