题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2604
题目意思:n个人排队,f表示女,m表示男,包含子串‘fmf’和‘fff’的序列为O队列,否则为E队列,有多少个序列为E队列。
思路:用f(n)表示n个人满足条件的结果,那么如果最后一个人是m的话,那么前n-1个满足条件即可,就是f(n-1),如果最后一个是f那么这个还无法推出结果,那么往前再考虑一位:那么后三位可能是:mmf, fmf, mff, fff,其中fff和fmf不满足题意所以我们不考虑,但是如果是 mmf的话那么前n-3可以找满足条件的即:f(n-3);如果是mff的话,再往前考虑一位的话只有mmff满足条件即:f(n-4) 所以f(n)=f(n-1)+f(n-3)+f(n-4),由于L非常大,所以使用矩阵快速幂。
构造一个矩阵: 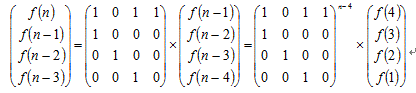
代码:

//Author: xiaowuga #include <bits/stdc++.h> #define maxx INT_MAX #define minn INT_MIN #define inf 0x3f3f3f3f #define n 4 using namespace std; typedef long long ll; int MOD; struct Matrix{ ll mat[4][4]; Matrix operator * (const Matrix & m) const{ Matrix tmp; for(int i=0;i<n;i++) for(int j=0;j<n;j++){ tmp.mat[i][j]=0; for(int k=0;k<n;k++){ tmp.mat[i][j]+=mat[i][k]*m.mat[k][j]%MOD; tmp.mat[i][j]%=MOD; } } return tmp; } }; Matrix POW(Matrix m,int k){ Matrix ans; memset(ans.mat,0,sizeof(ans.mat)); for(int i=0;i<n;i++) ans.mat[i][i]=1; while(k){ if(k&1) ans=ans*m; k/=2; m=m*m; } return ans; } int main() { ios::sync_with_stdio(false);cin.tie(0); int num; while(cin>>num>>MOD){ Matrix m; memset(m.mat,0,sizeof(m.mat)); for(int i=0;i<3;i++) m.mat[i][i+1]=1; m.mat[3][0]=m.mat[3][1]=m.mat[3][3]=1; m=POW(m,num-3); ll f[4]; f[0]=1; f[1]=2; f[2]=4; f[3]=6; if(num<=3) cout<<f[num]<<endl; else{ ll sum=0; for(int i=0;i<4;i++) sum+=m.mat[3][i]*f[i]%MOD; cout<<sum%MOD<<endl; } } return 0; }
