poj3735—Training little cats（特殊操作转化为矩阵操作）

题目链接：http://poj.org/problem?id=3735

题目意思：

调教猫咪：有n只饥渴的猫咪，现有一组羞耻连续操作，由k个操作组成，全部选自：

1. g i 给第i只猫咪一颗花生

2. e i 让第i只猫咪吃光它的花生

3. s i j 交换猫咪i与猫咪j的花生

现将上述一组连续操作做m次后，求每只猫咪有多少颗花生？

思路：这道题难点在如何把这种奇怪的操作转化为矩阵操作，网络上看到一个画的很好的图，这里直接偷过来。

 

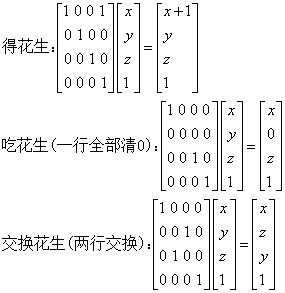
 现在，对于每一个操作我们都可以得到一个转置矩阵，把k个操作的矩阵相乘我们可以得到一个新的转置矩阵T。A * T 表示我们经过一组操作，类似我们可以得到经过m组操作的矩阵为 A * T ^ m,最终矩阵的[0][1~n]即为答案。

上述的做法比较直观，但是实现过于麻烦，因为要构造k个不同矩阵。有没有别的方法可以直接构造转置矩阵T？答案是肯定的。

我们还是以单位矩阵为基础：

对于第一种操作g i，我们使Mat[0][i] = Mat[0][i] + 1
对于第二种操作e i，我们使矩阵的第i列清零；
对于第三种操作s i j，我们使第i列与第j列互换。
这样实现的话，我们始终在处理一个矩阵，免去构造k个矩阵的麻烦。
至此，构造转置矩阵T就完成了，接下来只需用矩阵快速幂求出 A * T ^ m即可，还有一个注意的地方，该题需要用到long long。

这里还要说一下T*A=A*T的转置。

代码：

//Author: xiaowuga
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxx INT_MAX
#define minn INT_MIN
#define inf 0x3f3f3f3f
#define N  105
using namespace std;
typedef long long ll;
ll  n,size;//第n项，矩阵大小
struct Matrix{
    ll mat[N][N];
    void clear(){
        memset(mat,0,sizeof(mat));
    }
    Matrix operator * (const Matrix & m) const{
        Matrix tmp;
        int i ,j,k;
        tmp.clear();
        for( i=0;i<size;i++)
            for( k=0;k<size;k++){
                if(mat[i][k]==0) continue;
                for( j=0;j<size;j++){
                    tmp.mat[i][j]+=mat[i][k]*m.mat[k][j];
                }
            }
        return tmp;
    }
};
void POW(Matrix m,ll k){
    Matrix ans;
    memset(ans.mat,0,sizeof(ans.mat));
    for(int i=0;i<size;i++) ans.mat[i][i]=1;
    while(k){
        if(k&1) ans=ans*m;
        k/=2;
        m=m*m;
    }
    for(int i=1;i<size;i++){
        cout<<ans.mat[0][i]<<" ";
    }
    cout<<endl;
}
int main() {
    Matrix m;
    int k;
    while(cin>>size>>n>>k&&(size+n+k)){
        size++;
        m.clear();
        for(int i=0;i<size;i++) m.mat[i][i]=1;
        for(int i=0;i<k;i++){ 
            char t[5];
            int num1,num2;
            cin>>t;
            if(t[0]=='g'){
                cin>>num1;
                m.mat[0][num1]++;
            }
            else if(t[0]=='e'){
                cin>>num1;
                for(int j=0;j<size;j++){
                    m.mat[j][num1]=0;
                }
            }
            else{
                cin>>num1>>num2;
                for(int j=0;j<size;j++)
                    swap(m.mat[j][num1],m.mat[j][num2]);
            }
        }
        POW(m,n); 
    }
    return 0;
}