基本概念

 一. 什么是数据结构

解决问题方法的效率跟数据的组织方式有关

  图书馆放书：（考虑插入和查找的难易）

1. 随便放：
   1. 有空位就插入，易插；
   2. 需要遍历所有的图书，难找
2. 按照拼音字母顺序排放（插入时，所有插入之后的数据均需要后移一位，浪费；查找时，二分查找）；
   1. 二分查找确定位置，移出空位，但是当需要移动的量太多，会造成浪费；
   2. 二分查找
3. 按区域划分，区域内按照字母顺序排放（插入时，先分类别，二分查找确定位置，移出空位（移动数量和2相比少了很多）；
   1. 先分类别，二分查找确定位置，移出空位，与2相比，需要移动量会少
   2. 先分类别，再二分查找

解决问题方法的效率跟空间的利用效率有关

void PrintN101_1(int N)
{
    for (int i = 1; i <=N; i++)
    {
        printf("%d
", i);
    }
}

void PrintN101_2(int N)
{
    if (N)
    {
        PrintN101_2(N - 1);
        printf("%d
", N);
    }
}

第二种递归输出当N特别大时，会导致存储空间不够，溢出，递归函数吃掉所有空间，爆掉了

解决问题方法的效率跟算法的巧妙程度有关

多项式：f(x)=a₀+a₁x+...+a_n-1x^n-1+aⁿxⁿ；时间复杂度为T(n)=C₁n²+C₂n

double f103_1(int n, double a[], double x)
{
    int i;
    double p = a[0];
    for (i = 1; i <= n; i++)
        p += (a[i] * pow(x, i));
    return p;
}

提取上个多项式的公因式：f(x)=a₀+x(a₁+x(...(a_n-1+xaⁿ))...)); 时间复杂度为T(n)=C*n

double f103_2(int n, double a[], double x)
{
    int i;
    double p = a[0];
    for (i = n; i > n; i--)
        p = a[i - 1] + x * p;  
    return p;
}

第二种时间复杂度上面远远优于第一种方法

抽象数据类型

只描述数据对象集和相关操作集“是什么”，并不涉及“如何做到”的问题

clock()函数的返回类型为clock_t

注：函数运行时间太短，不到一个clock_t的时候，可以重复执行相同的函数，后进行平均

二. 什么是算法

算法描述不依赖于任何一种计算机语言以及具体实现的手段，不关心具体描述细节（伪代码）

空间复杂度：占用存储空间大小。PrintN101_2 函数中递归函数复杂度为C*N，由于每次递归都会占用一个新的内存空间，N过大内存不够用时会爆掉

时间复杂度：乘除耗时远大于加减

最坏复杂度：（最关心）T_worst(n)

平均复杂度: T_avg(n)    

T_avg(n)  < T_worst(n)

复杂度渐进表示法

log n<n<nlog n<n²<2ⁿ<n!

复杂度分析小窍门：

1. 若两段算法的复杂度相加，取较大的那一个；两端算法嵌套，则复杂度相乘；
2. n的k阶多项式的复杂度取最高阶的复杂度
3. for循环的复杂度等于循环次数乘以循环体代码的复杂度
4. if-else复杂度取决与条件判断复杂度和两个分支的复杂度，总体复杂度取其中最大的

 三. 案例

给定N个整数的序列{A₁,A₂,...,A_N},求子序列的最大和的序列

算法一：循环遍历求出每个子序列的和

int MaxSubseqSum130_1(int A[], int N)
{
    int ThisSum, MaxSum = 0;
    for (int i = 0; i < N; i++)
    {
        for (int j = i; j < N; j++)
        {
            ThisSum = 0;
            for (int  k = i; k < j ; k++)
            {
                ThisSum += A[k];
            }
            if (ThisSum > MaxSum)
                MaxSum = ThisSum;
        }
    }
    return MaxSum;
}

此时的时间复杂度为T(N)=O(N³)

算法二：算法一的第三层循环可以舍去，因为随着 j 的每次增加与上一个子序列的差值就只差增加的那一项，所以可以在之前的基础上直接加上当前项

int MaxSubseqSum130_2(int A[], int N)
{
    int ThisSum, MaxSum = 0;
    for (int i = 0; i < N; i++)
    {
        ThisSum = 0;
        for (int j = i; j < N; j++)
        {
            ThisSum += A[j]; //随着 j 的每次增加与上一个子序列的差值就只差增加的那一项
            if (ThisSum > MaxSum)
                MaxSum = ThisSum;
        }
    }
    return MaxSum;
}

此时算法的复杂度为T(N)=O(N²)。每当这时，考虑能不能把时间复杂度再往下降。

算法三. 分而治之：不断二等分递归

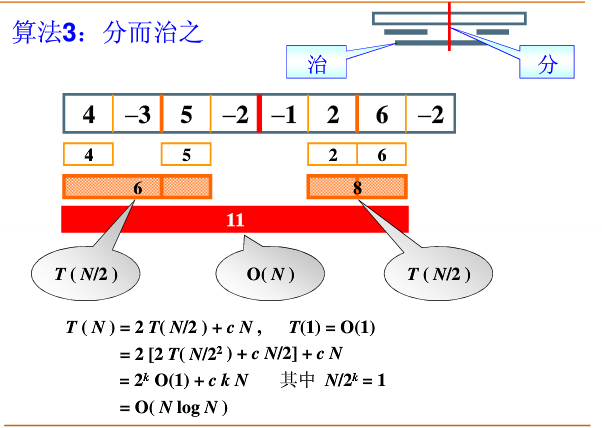
先不断二分求出其中每一部分的最大子序列之和，并且求出分割处最大子序列之和，三者比较保留最大的那个数

此时算法的复杂度为T(N)=O(NlogN)

算法四. 在线处理：即时处理

int MaxSubseqSum130_4(int A[], int N)
{
    int ThisSum=0, MaxSum = 0;
    for (int i = 0; i < N; i++)
    {
        ThisSum += A[i];
        if (ThisSum > MaxSum)
            MaxSum = ThisSum;
        else if (ThisSum < 0)  //如果当前子列和为负数
            ThisSum = 0;       //则不可能使后面的部分和增大，抛弃之
    }
    return MaxSum;
}

此时的时间复杂度：T(N)=O(N)

综上所述，算法四的时间复杂度最低