DP&图论 DAY 6 下午 考试

DP&图论  DAY 6  下午  考试

3
5 10 3
1 3 437
1 2 282
1 5 328
1 2 519
1 2 990
2 3 837
2 4 267
2 3 502
3 5 613
4 5 132
1 3 4
10 13 4
1 6 484
1 3 342
2 3 695
2 3 791
2 8 974
3 9 526
4 9 584
4 7 550
5 9 914
6 7 444
6 8 779
6 10 350
8 8 394
9 10 3 7
10 9 4
1 2 330
1 3 374
1 6 194
2 4 395
2 5 970
2 10 117
3 8 209
4 9 253
5 7 864
8 5 10 6

437
526
641

题解

>50 pt      dij 跑暴力 

               （Floyd太慢了QWQ    O（n^3））

                枚举每个点作为起点，dijkstra，跑暴力  O( (n+m)logn )，寻找全局最短路

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

typedef pair<int,int> pa;
const int maxn=1e5+10;
const int maxm=2e5+10;
int T;
int n,m,k;
struct node
{
    int to,nxt,dis;
}edge[maxm];
int head[maxn],cnt=0;
void addedge(int u,int v,int w)
{
    edge[++cnt].to =v;edge[cnt].dis =w;edge[cnt].nxt =head[u];head[u]=cnt;
    edge[++cnt].to =u;edge[cnt].dis =w;edge[cnt].nxt =head[v];head[v]=cnt;
}
int dis[maxn];
int a[maxn];

void dijkstra(int s)
{
    priority_queue<pa,vector<pa>,greater<pa> >q;
    q.push(make_pair(s,dis[s]=0));
    while(!q.empty() )
    {
        pa now=q.top();
        q.pop() ;
        if(now.second !=dis[now.first ]) continue;
        for(int i=head[now.first ],v;i;i=edge[i].nxt )
        {
            if(v=edge[i].to ,dis[v]>dis[now.first ]+edge[i].dis )
              q.push(make_pair(v,dis[v]=dis[now.first]+edge[i].dis));       
        }
    }
}

int main()
{
    T=read();
    for(int t=1;t<=T;t++)
    {
        cnt=0;
        memset(head,0,sizeof(head));
        memset(edge,0,sizeof(edge));
        memset(a,0,sizeof(a));
        n=read();m=read();k=read();
        for(int i=1;i<=m;i++)
        {
            int u=read(),v=read(),w=read();
            addedge(u,v,w);
        }
        
        for(int i=1;i<=k;i++) a[i]=read();
        int ans=0x3f3f3f3f;
        for(int i=1;i<=k;i++)
        {
            memset(dis,0x3f,sizeof(dis));
            dijkstra(a[i]);
            for(int j=1;j<=k;j++)
            {
                   if(a[i]==a[j]) continue;
                   ans=min(ans,dis[a[j]]);
            }
        } 
        if(ans>=0x3f3f3f3f) ans=-1;
        printf("%d
",ans);
        
    }
    return 0;
}

>100pt    考虑优化枚举量

因为答案是两个编号不同的点，所以对应的二进制编码至少有一位不同

枚举二进制的每一位

假设枚举到第 i 位，把这一位是 0 的点设置为源点，是 1  的设置为汇点，跑一遍多源多汇最短路

设置一个超级源点，向所有第一层集合的点连一条长度为 0 的边

设置一个超级汇点，所有最后一个集合的点向超级汇点连一条长度为 0  的边

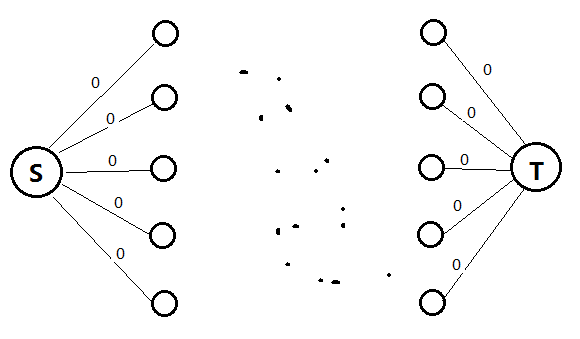
跑从超级源点到超级汇点的最短路

跑最多32次就可以得到答案

这两个集合既可以是 1~n ，也可以是 1~k 

显然 1~k 更优

#include <queue>
#include <cstdio>
#include <cstring>

template <class cls>
inline cls min(const cls & a, const cls & b) {
    return a < b ? a : b;
}   //定义一个取min

const int mxn = 100005;
const int mxm = 500005;
const int inf = 0x3f3f3f3f;

int n, m, k;

int points[mxn];  //存党员 

int tot;
int hd[mxn];
int nt[mxm];
int to[mxm];
int vl[mxm];

inline void add_edge(int u, int v, int w) {  //加边
    nt[++tot] = hd[u];
    to[tot] = v;
    vl[tot] = w;
    hd[u] = tot;
}

int dis[mxn];

struct data {
    int u, d;

    data(int _u, int _d) :
        u(_u), d(_d) {}
    
    bool operator < (const data & that) const {
        return d > that.d;
    }
};   //跑dijkstra的结构体

std::priority_queue<data> heap;

int main() {
    int cas;
    scanf("%d", &cas);  //多次询问
    for (int c = 0; c < cas; ++c) {
        
        //读边，存边
        scanf("%d%d%d", &n, &m, &k);  
        memset(hd, 0, sizeof(int) * (n + 5)); tot = 0;
        for (int i = 0, u, v, w; i < m; ++i) {  
            scanf("%d%d%d", &u, &v, &w);
            add_edge(u, v, w);
            add_edge(v, u, w);
        }

        //读入党员
        for (int i = 0; i < k; ++i)
            scanf("%d", points + i);
        int ans = inf;
        
        //对k进行二进制枚举
        for (int i = 1; i < k; i <<= 1) {
            memset(dis, inf, sizeof(int) * (n + 5));
            
            //枚举第i位上是0的党员存进去       
            for (int j = 0, p; j < k; ++j)
                if (p = points[j], (j & i) == 0)
                    heap.push(data(p, dis[p] = 0));
            
            //跑dijkstra        
            while (!heap.empty()) {
                int u = heap.top().u;
                int d = heap.top().d;
                heap.pop();
                if (dis[u] != d)
                    continue;
                for (int e = hd[u], v, w; e; e = nt[e])
                    if (v = to[e], w = vl[e], dis[v] > d + w)
                        heap.push(data(v, dis[v] = d + w));
            }
            
            //枚举第i位上是1的党员 
            for (int j = 0, p; j < k; ++j)
                if (p = points[j], (j & i) != 0)
                    ans = min(ans, dis[p]);
        }

        printf("%d
", ans == inf ? -1 : ans);

    }
    return 0;
}

  · flag 加了一点优化跑过了标程 

遇到一个就停了

---

 

3
5 10 5
4 10 8 1 10
1 3
1 4
1 5
1 3
2 1
2 5
4 3
4 3
4 5
5 1
1 4
4 6
1 9
4 7
2 9
5 10 5
2 8 8 10 10
2 1
2 3
3 2
3 4
3 1
3 2
3 4
4 1
5 4
5 1
1 4
2 3
4 7
3 10
1 5
5 10 5
9 9 8 2 1
1 5
1 5
2 1
2 4
2 4
2 4
3 2
3 1
4 3
4 3
5 9
3 9
2 7
5 1
5 4

40
60
90
70
90
8
30
70
100
10
9
81
63
14

 题解

 50pt    dfs  暴力

观察题目发现我们只需要找到对于一个点的 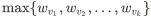 就好

#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<queue>

using namespace std;

typedef long long ll;

inline ll read()
{
    ll ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const ll maxn=2e5+10;
const ll maxm=4e5+10;
ll T;
ll n,m,k;
ll w[maxn],son[maxn];
ll head[maxn],to[maxm],nxt[maxn];
bool vis[maxn];

void addedge(ll u,ll v,ll cnt)
{
    to[cnt]=v;nxt[cnt]=head[u];head[u]=cnt;
}

void chuli(ll u)
{
    if(head[u]==0) return;
    if(vis[u]) return;
    vis[u]=1;
    for(ll i=head[u];i;i=nxt[i])
    {
        ll v=to[i];
        chuli(v);
        if(w[son[v]]>w[son[u]]) son[u]=son[v];
    }
    return;
}

int main()
{
//    freopen("neural.in","r",stdin);
//    freopen("ceshi.txt","w",stdout);
    T=read();
    for(ll t=1;t<=T;t++)
    {
        memset(w,0,sizeof(w));
        memset(son,0,sizeof(son));
        memset(head,0,sizeof(head));
        memset(nxt,0,sizeof(nxt));
        memset(to,0,sizeof(to));
        memset(vis,0,sizeof(vis));
        
        n=read();m=read();k=read();
        for(ll i=1;i<=n;i++)
           w[i]=read(),son[i]=i;
        for(ll i=1;i<=m;i++)
        {
            ll u,v;
            u=read();v=read();
            addedge(u,v,i);
        } 
        for(ll i=1;i<=n;i++) chuli(i);
        for(ll i=1;i<=k;i++)
        {
            ll u,x;
            u=read();x=read();
            printf("%lld
",(long long)x*w[son[u]]);
        }
    }
    return 0;
}

>100pt 

建反向边，tarjan然后拓扑就行了

(   然后我们发现一个大佬ych的思路

    思路是tarjan缩点，一个强连通分量的初始ans就是这个强连通分量里面点的最大值。然后建立新图，找到入度为0的点开始dfs，然后更新强连通分量的ans。

    询问点就是找点所在的强连通分量，输出强连通分量的ans就ok  )

#include <cstdio>
#include <cstring>

//自定义min  max 
template <class cls>
inline cls min(const cls & a, const cls & b) {
    return a < b ? a : b;
}

template <class cls>
inline cls max(const cls & a, const cls & b) {
    return a > b ? a : b;
}

const int mxn = 200005;
const int mxm = 400005;

int n, m, k, w[mxn];

struct edge {
    int u, v;
} edges[mxm];

int tot;
int hd[mxn];
int to[mxm << 1];
int nt[mxm << 1];

inline void add_edge(int u, int v) {
    nt[++tot] = hd[u];
    to[tot] = v;
    hd[u] = tot;
}

int tim;
int cnt;
int top;
int dfn[mxn];
int low[mxn];
int stk[mxn];
int scc[mxn];

void tarjan(int u) {
    dfn[u] = low[u] = ++tim; stk[++top] = u;
    for (int e = hd[u], v; e; e = nt[e])
        if (v = to[e], scc[v] == 0) {
            if (dfn[v] == 0)tarjan(v),
                low[u] = min(low[u], low[v]);
            else
                low[u] = min(low[u], dfn[v]);
        }
    if (dfn[u] == low[u]) {
        cnt += 1;
        do {
            scc[stk[top]] = cnt;
        } while (stk[top--] != u);
    }
}

int oe[mxn];  //in[ ]  
int mx[mxn];  //每个强连通分量内部最大 w  

int que[mxn];

void bfs() {
    int l = 0, r = 0;
    for (int i = 1; i <= cnt; ++i)
        if (oe[i] == 0)
            que[r++] = i;
    
    while (l < r) {
        int u = que[l++];
        for (int e = hd[u], v; e; e = nt[e])  //注意边是反向建的
            if (v = to[e], mx[v] = max(mx[v], mx[u]), --oe[v] == 0)
                que[r++] = v;
    }
}

int main() {
    int cas;
    scanf("%d", &cas);
    for (int c = 0; c < cas; ++c) {
        
        scanf("%d%d%d", &n, &m, &k);
        for (int i = 1; i <= n; ++i)
            scanf("%d", w + i);
        
        //连边建图    
        memset(hd, 0, sizeof(int) * (n + 5)); tot = 0;
        for (int i = 0; i < m; ++i) {
            scanf("%d%d", &edges[i].u, &edges[i].v);
            add_edge(edges[i].u, edges[i].v);
        }
        
        //tarjan缩点 
        tim = cnt = top = 0;
        memset(scc, 0, sizeof(int) * (n + 5));
        memset(dfn, 0, sizeof(int) * (n + 5));
        for (int i = 1; i <= n; ++i)
            if (scc[i] == 0)
                tarjan(i);
        
        //缩点之后重新连边建图        
        memset(hd, 0, sizeof(int) * (cnt + 5)); tot = 0;
        memset(oe, 0, sizeof(int) * (cnt + 5));
        memset(mx, 0, sizeof(int) * (cnt + 5));
        for (int i = 0; i < m; ++i) {
            int u = scc[edges[i].u];
            int v = scc[edges[i].v];
            if (u != v) 
                add_edge(v, u), oe[u] += 1;   //建反向边
        }
        
        //每个强连通分量内部的最大 w 值 
        for (int i = 1; i <= n; ++i)
            mx[scc[i]] = max(mx[scc[i]], w[i]);
            
        bfs();  //topsort求每个点可达的最大w 
        
        for (int i = 0, u, x; i < k; ++i) {
            scanf("%d%d", &u, &x);
            printf("%lld
", 1LL * x * mx[scc[u]]);
        }
        
    }
    return 0;
}

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<queue>

using namespace std;

inline int read()
{
    int ans=0;
    char last=' ',ch=getchar();
    while(ch<'0'||ch>'9') last=ch,ch=getchar();
    while(ch>='0'&&ch<='9') ans=ans*10+ch-'0',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

const int maxn=200005;
const int maxm=400005;
int T;
int n,m,k,w[maxn];
int head[maxn],to[maxm<<1],nxt[maxm<<1],edge_num=0;
struct node
{
    int u,v;
}edge[maxm];

void addedge(int u,int v)
{
    to[++edge_num]=v;nxt[edge_num]=head[u];head[u]=edge_num;
}

int dfn[maxn],low[maxn],scc[maxn],sta[maxn],top=0,tim=0,scc_num=0;

void tarjan(int u)
{
    dfn[u]=low[u]=++tim;
    sta[++top]=u;
    for(int i=head[u],v;i;i=nxt[i] )
    {
        v=to[i] ;
        if(!scc[v])
        {
            if(!dfn[v])
               tarjan(v),low[u]=min(low[u],low[v]);
            else
               low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u])
    {
        scc_num++;
        int y;
        do
        {
            y=sta[top--];
            scc[y]=scc_num;
        }while(y!=u);
    }
}

int in[maxn],mxn[maxn];

void topsort()
{
    queue<int>q;
    for(int i=1;i<=scc_num;i++)
        if(!in[i]) 
           q.push(i); 
    
    while(!q.empty() )
    {
        int now=q.front() ;
        q.pop() ;
        for(int i=head[now];i;i=nxt[i])
        {    
            int v=to[i];
            mxn[v]=max(mxn[now],mxn[v]);
            in[v]--;
            if(!in[v]) q.push(v); 
        }
    }
}

int main()
{
    T=read(); 
    for(int t=1;t<=T;t++)
    {
        n=read();m=read();k=read();
        for(int i=1;i<=n;i++) w[i]=read();
        memset(head,0,sizeof(head)); edge_num=0;
        for(int i=1;i<=m;i++)
        {
            edge[i].u =read();edge[i].v =read();
            addedge(edge[i].u,edge[i].v);
        }   
        
        tim=top=scc_num=0;
        memset(dfn,0,sizeof(dfn));
        memset(scc,0,sizeof(scc));
        memset(low,0,sizeof(low));
        memset(sta,0,sizeof(sta));
        for(int i=1;i<=n;i++)
          if(!scc[i]) 
            tarjan(i);
        
        memset(head,0,sizeof(head)); edge_num=0;
        memset(to,0,sizeof(to));
        memset(nxt,0,sizeof(nxt));
        memset(in,0,sizeof(in));
        memset(mxn,0,sizeof(mxn));
        for(int i=1;i<=m;i++)
        {
            int u=scc[edge[i].u ];
            int v=scc[edge[i].v];
            if(scc[u]!=scc[v])
              addedge(v,u),in[u]++;
        }
        for(int i=1;i<=n;i++)
          mxn[scc[i]]=max(mxn[scc[i]],w[i]);
        topsort();
        for(int i=1,u,x;i<=k;i++)
        {
            u=read();x=read();
            printf("%lld
",(long long)x*mxn[scc[u]]);
        }
        
    }
    return 0;
}

---

 

2
3
1
0
2
0
2
2
1
0

题解

很像 Qtree 啊 所以一样hintai

----------------------------------------------------

树链剖分

单点修改，查询区间内值为x的数

考虑如何实现？？？

如果x比较少，完全可以建几棵线段树来实现，就好比 20% 的数据，颜色种类不超过 5 

每次修改一个颜色，就是在该颜色线段树内 +1，原颜色线段树内 -1 

颜色种类多了怎么办？

暴力：开100个树状数组，和刚才没什么区别

如果线段树在每一个节点上维护一个100的数组

合并的时候可以直接暴力统计节点次数，这样代价是区间长度

如果每一位枚举则是n*100

每一层访问的点是n的，一共log层

复杂度 O（nlogn）

继续优化：

离线操作，只需要建一棵线段树

操作分类，与同一种颜色有关的操作放到一起

所有操作次数相加就是2m

所以操作还是o(m)

 ---------------------------------------------------------

另一种不用树剖的方法

把节点按照DFS序排下来，一个点修改的时候会对他所有子树产生影响

查询的时候 (a-->root)+(b-->root)-(lca(a,b)-->root)+(lca(a,b))

开100个树状数组

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

inline int getint()  //快读 
{
    int r = 0, c = getchar();
    
    for (; c < 48; c = getchar());
    for (; c > 47; c = getchar())
        r = r * 10 + c - 48;
    
    return r;
}

const int mxc = 100005;
const int mxn = 100005;
const int mxm = 200005;

int n, m, c;

int tt;
int hd[mxn];
int to[mxm];
int nt[mxm];
inline void addedge(int x, int y)
{
    nt[++tt] = hd[x], to[tt] = y, hd[x] = tt;
    nt[++tt] = hd[y], to[tt] = x, hd[y] = tt;
}

struct data
{
    int k,   //操作顺序编号 
        x,   //1：位置  2：查询区间左端点 
        y;   //1：修改的颜色  2：查询区间右端点 
    
    data() {} ;
    data(int a, int b, int c)
        : k(a), x(b), y(c) {} ;
};

int color[mxn];

#include <vector>

vector<data> vec[mxc];

int tim;
int dfn[mxn];
int top[mxn];
int fat[mxn];
int dep[mxn];
int son[mxn];
int siz[mxn];

void dfs1(int u, int f)  //更新size,son,(dep,fa) 
{
    siz[u] = 1;
    son[u] = 0;
    fat[u] = f;
    dep[u] = dep[f] + 1;
    
    for (int i = hd[u], v; i; i = nt[i])
        if (v = to[i], v != f)
        {
            dfs1(v, u);
            siz[u] += siz[v];
            if (siz[v] > siz[son[u]])
                son[u] = v;
        }
}

void dfs2(int u, int f)  //更新dfn,top 
{
    dfn[u] = ++tim;
    
    top[u] = ( son[f] == u ? top[f] : u ); 
    
    if (son[u])
        dfs2(son[u], u);
    
    for (int i = hd[u], v; i; i = nt[i])
        if (v = to[i], v != f && v != son[u])
            dfs2(v, u);
}

int bit[mxn];

inline void add(int p, int v)  //树状数组维护，位置p上+v 
{
    for (; p <= n; p += p & -p)
        bit[p] += v;
}

inline int ask(int l, int r)  //树状数组查询 
{
    int sum = 0; --l;
    
    for (; r; r -= r & -r)
        sum += bit[r];
    
    for (; l; l -= l & -l)
        sum -= bit[l];
    
    return sum;
}

int ans[mxn];  //第i个操作的答案 

signed main()
{
    int cas = getint();
    
    while (cas--) 
    {
        n = getint();
        m = getint();
        
        for (int i = 1; i <= n; ++i)
            vec[color[i] = getint()].push_back(data(0, i, +1));
        
        c = 0;
        
        for (int i = 1; i <= n; ++i)  //一共有多少种颜色 
            c = max(c, color[i]);

        memset(hd, 0, sizeof(int) * (n + 5)); tt = 0;
        
        for (int i = 1; i < n; ++i) //连边 
        {
            int x = getint();
            int y = getint();
            
            addedge(x, y);
        }
        
        for (int i = 1; i <= m; ++i)
        {
            if (getint() == 1)
            {
                int p = getint();
                int a = color[p]; //p处的原色 
                int b = color[p] = getint(); //p处更改后的颜色 
                
                vec[a].push_back(data(0, p, -1));
                vec[b].push_back(data(0, p, +1));
            }
            else
            {
                int x = getint();
                int y = getint();
                int k = getint();
                
                vec[k].push_back(data(i, x, y));
            }
        }
        
        //树链剖分两遍dfs 
        dfs1(1, 0);
        dfs2(1, 0);
        
        memset(ans, -1, sizeof ans);
        
        for (int k = 1; k <= c; ++k)  //分别处理每一种颜色 
        {
            int sz = vec[k].size();   //操作总次数 
             
            memset(bit, 0, sizeof bit);
            
            for (int i = 0; i < sz; ++i)  //挨个处理操作 
            {
                const data &d = vec[k][i];  
                
                ans[d.k] = 0;  //初始化第d.k个操作的答案是0 
                
                if (d.k == 0)  //修改颜色 
                    add(dfn[d.x], d.y);
                else  //区间查询，树链剖分 
                {
                    int a = d.x, ta = top[a];
                    int b = d.y, tb = top[b];
                    
                    while (ta != tb)
                    {
                        if (dep[ta] >= dep[tb])
                            ans[d.k] += ask(dfn[ta], dfn[a]), ta = top[a = fat[ta]];
                        else
                            ans[d.k] += ask(dfn[tb], dfn[b]), tb = top[b = fat[tb]];
                    }
                    
                    if (dep[a] <= dep[b])
                        ans[d.k] += ask(dfn[a], dfn[b]);
                    else
                        ans[d.k] += ask(dfn[b], dfn[a]);
                }
                
                
            }
        }
        
        for (int i = 1; i <= m; ++i)   //离线输出答案 
            if (ans[i] >= 0)
                printf("%d
", ans[i]);

        for (int i = 1; i <= c; ++i)  //清空数组 
            vec[i].clear();
        
        tim = 0;
    }
    
    return 0;
}

---

树链剖分可以

单点加  查询路径权值和