一、基本概念
图(graph)是一种网状数据结构,图是由非空的顶点集合和一个描述顶点之间关系的集合组成。
图由顶点和边组成,顶点表示对象,边表示两个对象间的连接关系。
图大体分为两种,边没有指向性的叫无向图,边具有指向性的叫有向图。
方向起始的顶点称为起点或尾(弧尾)。方向指向的顶点称为终点或头(弧头)。
边可以带权值,称为带权图。
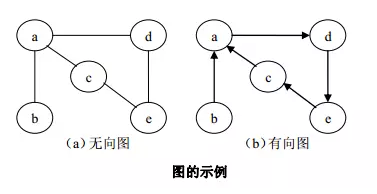
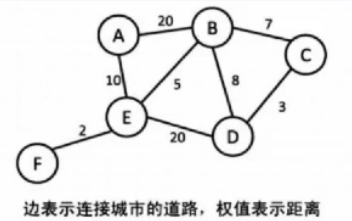
二、术语
有n(n-1)/2条边的无向图称为无向完全图。
有n(n-1)条边的有向图称为有向完全图。
有很少边的图称为稀疏图。
边较多的图称为稠密图。
两个顶点之间如果有边连接,视为两个顶点相邻。
相邻顶点的序列称为路径。

起点和终点重合的路径称为圈。
顶点连接的边数叫做这个顶点的度。
对有向图中某结点的弧头数称为该结点的入度(in degree)。
对有向图中某结点的弧尾数称为该结点的出度(out degree)。
有度=入度+出度

在无向图中,从一个顶点到另一个顶点之间有路径,则称这两个顶点是连通的。
任意两点之间都存在路径连接的图称为连通图

对于有向图,若两点之间有互相到达的路径,则称这两点是强连通。
如果有向图中任何一对顶点都是强连通的,则此图叫强连通图。
有向图中最大连通子图称为有向图的强连通分量。

三、树与图的关系
没有圈的连通图,就是树。
没有圈的非连通图,就是森林。
一棵树的边数等于顶点数-1。
边数等于顶点数-1的连通图,就是树 。
四、有向无环图
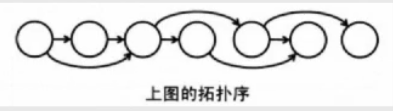
没有圈的有向图,叫做DAG(Directed Acyclic Graph,有向无环图)

拓扑排序定义:将DAG中的顶点以线性方式进行排序。即对于任何自顶点u到顶点v的有向边u->v,在最后的排序结果中,顶点u总是在顶点v的前面。这样的排序结果,称为拓扑序。