线性模型

线性模型最终训练出来的是w列向量；验证以及判断都是基于这个训练出来的w列向量进行的。所以，所谓的线性模型是指数据的分布大体是满足一次方程的；线性模型学习的结果就是把这个一次方程的w给获得，这样就可以得到一个模型了；未来只要向这个模型（一次方程）传入样本即可得到结果。模型是一个什么概念？总体来讲模型是一个盒子，具有输入输出口，你输入了样本数据，就会输出接过来，这个是模型的宏观样子；那么在这个盒子的里面，其实是一个函数，输入的参数将会被直接，或者处理后输入到这个函数中获得结果做返回；作为函数，那就是三部分：因变量（返回值y），自变量（x，样本特征值）以及系数（w，这个就是线性回归学习的主要目标）。这样才是一个模型的概念。

MLInAction这本书代码质量低下的一个体现就是没有很好的体现模型的概念，训练出来w列向量之后，直接拿来和test集数据作用，虽然没有错误，但是没有很好的提下出"模型"的概念，其实应该至少封装成一个函数，让他能够有输入输出的模型的样子啊；否则给人感觉就是一个半成品的样子，太糙了。

标准线性回归

线性回归，首先就是标准的回归模型，y = w.T * X；对于线性模型上面提到了目标就是解出来w，那么怎么解决w呢？一般都是采用最小二乘法：

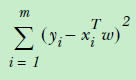
这个公式也称之为损失函数，目标就是达到损失函数最小情况下的w。为了便于计算，上面的公式又可以采用向量形式表达：

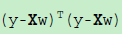
为了求出极值，那么我们可以对其求导，对于向量求导，牵涉到了泛函知识，这里就不详细推到了，总是求导之后，我们得出了w的极值（这里是极小值）：

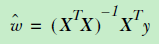
那么预测的时候，只要使用wHat * X（X是预测样本）就可以获得预测的值了。

python代码实现：

from numpy import mat
from numpy import linalg
# 根据公式求出w值，我们知道的是点集，下面我们需要搞掂的根据点集来推断出趋势来，也就是这一章的主题：预测。
# 那么我们就首先假设（或者说根据点集分布进行推测）数据是线性分布，那么它就满足y= w.T*x，因为点集就是有x,y组成，所以下面
# 我们需要求解的就是w，这里求解w采用的方式就是最小二乘法（OLS，ordinary least square），顾名思义，二乘法，两个数相乘，
# 在这里则是sum(yi - w.T*x)**2，为了求“最小”，下面我们对sum进行求导，可以得到最小值w=(x.T*x).I*x.T*y；该方法就是利用
# 这个求导后的最小值公式来求参数w
def standregres(xArr, yArr):
    xMat = mat(xArr)
    yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0:
        print("result is 0, can't invert")
        return
    ws = xTx.I * (xMat.T * yMat)
    
    return ws

回顾一下标准的线性回归：最小二乘法->向量形式表达->求导获得最小值表达形式，这我们只要把训练样本中的X和y传进去尽可以得到一个w的估计值（这里w上面的带了一个小帽子，代表估计）。OK，上诉算法就是标准的线性回归的算法；这个算法好处就是清晰，简单，但是缺点就是，因为模型太简单（太直男），所以欠拟合，对于一定曲线新装的数据分布不能很好的拟合。

局部加权线性回归

这个时候，需要引入局部加权线性回归（LWLR，Local Weight Linear Regression）。为什么不能很好拟合？因为标准线性回归走的是MSE（Min Square Error），这个时候需要引入一些偏差来减小误差,线性回归就是一条直线，局部加权则实现了曲线拟合。

 最上面是线性回归，可以看到就是一条直线，对于数据某种程度上欠拟合，中间的图是K值0.01，下图是K值0.003

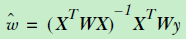
X和y前面都左乘了一个系数Weight，这个Weight是什么呢？这个weight很多时候采用的就是核。在svm曾经介绍过核的概念，主要是用于低维向高维映射实现分类区域划分；但是那个核函数是用于分类；在LWLR中核函数的作用就是作为权重，或者说用来增加偏差的，进而增强拟合的。

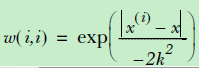
可以发现核函数是发生在对角线上面的，这样可以保证weight右乘X以及y之后，系数会作用在每一个样本对应的特征上面。注意，这个权重不是特征权重，而是样本权重，这里的x就是待预测的点，这里用到了曼哈顿距离，可以看到距离待预测点越近，赋予的权重就越大，这个是合理的。

注意，这里在计算过程中引入了待预测样本，因为需要核函数需要计算所有的训练样本和预测样本之间的距离；这意味着LWLR这种训练模型不具备共同性，必须要要预测样本参与才可以进行；但是这是不合理的；我觉得正确的处理方式还是基于训练数据把w训练出来；那么真正在预测的时候就是采用基于训练数据训练出来的数据进行预测即可。否则所有的预测都参与样本的训练是一件非常扯的事情。这个也是为什么我认为MLInAction代码写的烂的原因。

同样的，LWLR本质也是求解w，通过LWLR求解出了w之后，通过w*X可以求出。下面是python实现：

from numpy import eye
from numpy import mat
from numpy import exp
from numpy import linalg
# 基于本地权重计算预测值
# 注意这里X*Weight，之类weight是一个对角矩阵，根据矩阵乘法的规则，Weight矩阵的意义其实就是指定了每个特征的权重。
# 所以LWLR回归本质就是通过为特征赋权值来实现欠拟合到拟合的优化；那么问题来了，怎么设置这个权值呢？公式来了：
# exp(|xi - x|/-2k**2)
# 于是下面我们需要做到的就是通过调参来找到最佳参数k
# 这个函数其实实现了两个功能：根据xArr以及yArr训练出列权重矩阵weightp[]，然后返回测试数据的（参数sample）和w相乘的结果，这个结果
# 就是yHat，就是预测值！

# 外部通过这个返回值yHat和y真值进行比较，推断预测的水平怎么样。

# 另外这里关于矩阵乘法有一个隐喻：左乘的矩阵提供的是一个样本得特征，右乘的矩阵提供的特征的系数，所以样本和特征参数相乘，因为样本只是1个
# 所以结果上面来看，行数和左乘矩阵是一致，代表着样本数量是不会变得；列数确实和右乘矩阵一致，这是因为右乘矩阵代表对样本洗礼次数（通过
# 特征值和参数相乘），所以产生的是一个新的样本，这样样本代表了基于原来样本的N此洗礼处理。
def localWeightLinearRegression(sample, xArr, yArr, k):
    xMat = mat(xArr)
    yMat = mat(yArr)
    m = shape(xMat)[0]
    weight = mat(eye(m))
    for j in range(m):
        diff = sample - xMat[j, :]
        weight[j, j] = exp(diff*diff.T / (-2.0*k**2))
    xTx = xMat.T * (weight * xMat)
    if(linalg.det(xTx) == 0):
        print("det is zero, return")
        return
    wHat = xTx.I * (xMat.T * (weight * yMat.T))
    
    return sample * wHat

岭回归

无论是标准的回归还是LWLR求解w都要面对一个问题，即使当矩阵不满秩的时候，无法求出其逆矩阵；所谓不满秩就是指样本数小于特征数，这个时候就需要对原有模型进行一些调整，这里就有了岭回归和LASSO回归。

岭回归的原始公式如下：

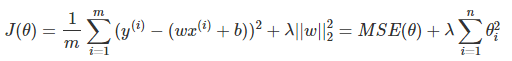
求导之后：

注意这里的θ就是上文中w。这里看到公式多了一个λ*I，I是一个单位矩阵（对角矩阵且只有对角线值为1，其他位置都是0）；用于避免X.T*X为0的情况发生。例如：

# 用于验证，对于一个特征数量大于样本数量的场景，linalg.det是否为0
aMat = mat(ones((5,2)))
tMat = aMat.T
print("tMat*aMat")
print(tMat*aMat)
det = linalg.det(tMat*aMat)
print("det:")
print(det)

# 验证一下det为0的方阵添加一个单位矩阵之后是否就会det不等于0
eyeMat = mat(eye((2)))
print("init eyeMat: ")
print(eyeMat)
print("tMat*aMat + eyeMat")
print(tMat*aMat + eyeMat * 0.05)
det = linalg.det(tMat*aMat + eyeMat * 0.05)
print("added I, the det:")
print(det)

上述代码执行只有可以发现添加了λ*I之后，det确实不再等于0了。

岭回归另外一个作用就是减少缺少影响y值的特征的权重的作用；但是岭回归更多的做得是减少，下面我们介绍另外一种回归：LASSO回归。

LASSO回归

LASSO回归和岭回归比较类似，但是LASSO对于w的减弱做得更狠一些，就是会直接将其降为0；

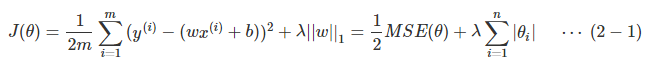
两种的差别在于正则项在LASSO里面是L1的，在岭回归则是L2；因为LASSO会将权重下降为0，所以采用LASSO在一定程度上起到了降维的作用。