决策树算法
如何能够基于既有的数据来进行分类和回归?决策树是解决这类问题的机器学习模型。
解决思路是:通过样本特征的三个数字特征:1)满足特征值的样本数量;2)1)样本的分类各自数量有多该少;3)总的样本数量,来作为input参数,通过构建/选择的模型就计算出来该特征的指标,对于ID3而是信息增益,C4.5是最大信息增益比,CART则是gini指数;有了一系列特征指标之后,从中按照某种规则(比如指标最大)来挑选节点(节点值),然后剔除掉这个特征,再从剩下的特征中再选择其孩子节点是哪个1。
决策树算法(启发函数)包括:ID3,C4.5以及CART,scikit learn的Decision Tree实现的是CART,这也说明CART是最重要的算法。这里为什么叫启发式函数?就是因为其实采用各种函数,其实并不一定能够保证是最优划分,只是一种划分的方式,后续还需要通过类似于剪枝,重新构建等方式来对树的节点进行优化。
ID3只用于离散的分类;C4.5可以用于基于连续值的分类,其原理是将连续值进行数据分段,针对每一段进行作为节点划分;CART则是不仅可以用于各种类型数据的分类(连续好离散的),还可以用于回归分析(这一点通过Class And Regression Tree的命名可以看到),这里CART对于连续值的处理C4.5是一致的;
三者之间的关系也是递进的;ID3算法是基于最大信息增益,什么是信息增益?首先要明白经验熵,熵描述的是研究对象活跃度的数字,从物理学(热力学)角度来讲,熵是什么呢?熵是微观状态空间某集合中所包含的点的数目之对数,这些点对应于一个同样的宏观态( n )。 在信息学领域,香农借鉴了这个概念,用来熵这个概念描述信息的不确定度,熵值越高,代表越不确定。
比如,“今天太阳会升起”,这个是100%会发生的事情,没有什么不确定性,那么熵值就小;但是如果”今天会有一个妹子向我表白“,这种发生概率比较小的事情,信息量就是比较大,同理掷骰子的熵值就是要高于投硬币,前者概率是1/6,后者是1/2。所以熵的定义为:对于(描述的)信息预期,对平均不确定性的度量。定义为:
![]()
描述分类熵值的公式如下所示:
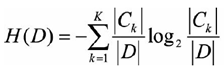
数据集D中,分类Ck的熵值之和就是数据集D的熵值;注意,这的分类指的是响应量,即Y值;比如一个100个相亲样本,重点培养有20个,不见有30,相处看看有50个,那么C0 = 20,C1=30,C2=50,D=100。这里的Cx都是指(分类)监督学习里面的Label。
描述指定特征A的经验熵值如下:
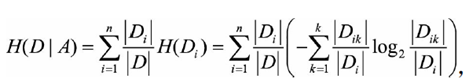
Di代表取特征A的第i个的特征值的样本集合(D的子集),这里n代表特征A的特征值的个数,Dik代表第i个特征,其中属于第k个分类的样本集合;举个例子,100个人(样本D),国籍(特征A)为中国人(i=0)50个,美国人(i=1)30个,韩国人(i=2)20个;其中50个中国人中青年人(k=1)为15个,男人(k=2)26个;那么D=100,D1=50,D2=30,D3=20,D11=15,D12=26。
你会发现,分类熵等于所有的特征的经验熵之和,这个也是经验熵公式来历:
H(D) = H(D|A)+H(D|B)+H(D|C)+...
作为经验熵公式,H(D|A)这个公式仔细体会一下,会发现其实它描述的就是指定的特征值作为分割点之后,每个特征值节点(叶子节点)的样本分类稳定性(叶子节点的样本的分类是否比较简单,明确)
信息增益描述的是指定特征的确定性,增益越大说明特征越稳定(注意这个增益是整体相对于指定特征的,越大说明特征的稳定),公式如下:
g(D, A) = H(D) - H(D|A)
这样信息增益越大=>熵值越小=>确定性越高,这里熵值其实代表的混杂度(不确定性),在分类中混杂度描述的一个叶子节点的样本总体,分类是否明确,越明确(某个分类的样本数量绝对有事)则增益越大;混杂度越低,纯洁度越高,所以要选择信息增益最大的那个字段作为区分字段,这意味着当使用这个字段来做分支的时候,各个分支下面的节点(可能是叶子节点)分类最明确(概率值最大);当然极端的直接的将该字段作为叶子节点的父节点,旗下直接就是分类结果;
但是这样的决策有一个缺点,就是你会发现因为公式是Xlog2X,具有越多的特征值的特征,每个特征值的熵值较小,导致其H(D|A)越小,比较极端情况,如果是选取ID特征做研究,因为所有的样本都是只有唯一值,所以log值为0(Dik=1,Di=1,Dik/Di = 1)。
C4.5在算法方面做了改善,不在仅仅看信息增益,而是看信息增益和D关于A的取值熵的比值,有了这个比值,一定程度上削减了多特征值对于结果的影响。
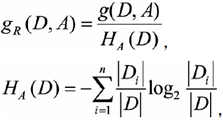
上述公式中Di是特征A的第i个特征值,其含义和上面描述的Dik是一样的;HA(D)则是代表特征A的熵(所有分类的熵),注意这里HA(D)前面是一个负号,负号进入到log里面就意味着分子分母互换位置,这样,HA(D)就变大了,所以相当于H(D|A)越小,G(D,A)是越大的,但是分母HA(D)也是更加的大,所以在H(D|A)计算过程中因为特征值多而占的“便宜”,会因为分母除以了同步变大的值,而得以一定程度的抵消(惩罚)。
CART采用的度量对象时Gini指数,很多书籍描述其为纯度,其实解释为"混杂度"更加合适一些(或者说不确定性,其实和熵的概念类似),因为Gini指数=0,代表纯度最高(稳定性确定性最好)。
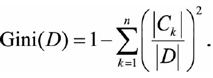
CART在构建树的时候,每次都是选择gini指数最小(稳定性好的)的特征的条件来作为二叉树的节点来进行构建(CART的树和ID3以及C4.5之间的区别还在于CART是一棵二叉树):
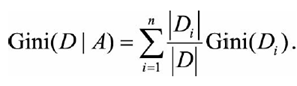
另外,在构建决策树的时候,可能很多时候都不一样,这个是因为在每次构建决策树的时候,取出的构建样本都不一样,可能会导致特征对应的特征数字会有出入,所以会不一样,比如在随机森林里面,每次都是用一部分的数据来构建子树,然后放回采样构建下一颗子树,所以会有森林里面的决策树都不一样的。
关于决策树的决策概率
在分类模型上,因为决策树节点大部分都是不纯洁的,所以在使用训练样本构建树的时候,最终在各个叶子结点上的样本一部分是A分类,一部分B分类等等,那么这意味着在每个叶子节点上,每个分类是有一定概率的(基于此次样本训练出来的结果),假设是一个二分类的模型,针对某个叶子结点,最终落入了100个训练样本,A分类是80个,B分类是20个;如果我们使用predict返回的当然的是A分类,但是对于决策树还提供了一个predict_proba函数,通过这个函数可以知道预测的每种分类(A:80%,B: 20%)的概率是怎么样的;
关于剪枝(Pruning)
构建决策树的问题:树的构建是会过拟合的(测试集表现得很好,但是验证集表现比较差),所以需要对树进行剪枝来提高其泛华能力;构建树的启发式算法有研究表明差别并不是很大(毕竟大家都是启发式的算法,并非最优算法),关键在于剪枝。
剪枝有两种方式,分别是预剪枝(pre-pruning)和后剪枝(post-pruning)。
预剪枝
预剪枝是通过设定一些参数,让其在构建树的过程中,一些超参数达到了阈值之后,就停止构建树。这里包括:
max_depth: 最大深度;当数据量比较少的时候,可以不管这个参数,但是如果数据量非常大,会导致深度过深进而影响学习效果,需要对深度进行控制;
min_samples_split: 指定某个节点的样本数少于阈值,将不会再进行分割,即样本过少,只能作为叶子节点;
max_leaf_nodes: 限制最大叶子节点数量。如果特征不多,可以不考虑这个参数;如果特征过多进而导致了叶子节点众多,竟可能会导致过拟合,此时需要考虑限制最大叶子数量,一定程度上和max_depth的效果类似,限制叶子节点的数量也是间接的在一定程度上限制深度;
min_samples_leaf: 指定了叶子节点最小数量,小于该阈值的叶子节点,将会自动被剪枝(归并到上级节点)
后剪枝
解决过拟合的方案:剪枝本质就是删掉一些叶子节点,让父节点成为叶子节点,让剪之后的叶子节点更加憨厚,泛华性好一些。
方案的实现:剪枝有很多算法,这里讲一下CART的CCP(Cost Complexity Pruning,代价复杂度)算法,原理是对所有的父节点(非叶子节点)都计算一下减去其子节点前后的误差值,计算误差增加率:
α = [R(t) - R(T)] / (|L(T)| - 1)
其中alpha值最小的节点,剪掉其子节点。为什么选择最小的呢?说明其子节点进行细化分支的价值并不是很明显。所以直接剪去;然后继续遍历计算误差增加率,选择最小的进行剪枝,迭代进行,一直到最小的α<=0剪枝结束,因为这意味再剪下去已经没有意义了。
推广
其实你会发现决策树的过程和梯度下降类似,首先二者都是启发式的建模过程,通过迭代来求得局部最优;对于决策树而言,基于熵值,gini值等来判断特征的稳定程度,基于启发式函数来决定谁来作为分支节点,然后通过剪枝来进行迭代优化;对于梯度喜爱而言,则是开始启发式的指定参数θ值,然后通过计算梯度值来获得下一个调整θ值;两者都无法通过穷举获得最优解,只是通过局部最优来作为最终结果。
其实,从本质上面来讲二者都是贪心算法,因为每一步选择的都是局部优化,即当前指标值最好的,比如在决策树,每次节点的划分都是信息增益/比值/gini指数最大最小;对于梯度下降,参数θ每次变化的方向都是切线方向,或者说变小的方向,当然对于Line regression的损失函数是凸函数,这种方式可以找到全局最低点,但是对于其他形式的曲线,则碰到的第一个低点(第一次损失函数增值了)不一定是最全局最低点。诸如此类
另外,对于CART的回归实现,是另外一套基于损失函数最小化的算法,这个另外再写一篇文章来说明。
参考:
关于熵,信息增益以及信息增益率
https://blog.csdn.net/u012351768/article/details/73469813
https://blog.csdn.net/qintian888/article/details/90054519
关于分类的算法
《百面机器学习》
《Scikit-learn与Tensorflow》
比如,“今天太阳会升起”,这个是100%会发生的事情,没有什么不确定性,那么熵值就小;但是如果”今天会有一个妹子向我表白“,这种发生概率比较小的事情,信息量就是比较大,同理掷骰子的熵值就是要高于投硬币,前者概率是1/6,后者是1/2。所以熵的定义为:对于(描述的)信息预期,对平均不确定性的度量。定义为: