算法练习——堆排序

堆是一个数据结构，可以看作是一个数组，并且具有完全二叉树的性质，每个结点都对应一个数组的元素。

堆和数组对应的关系类似于一种层序排列。

比如：对于数组   A= {27,17,16,13,10,1,5,7,12,14,8,9}

A数组在堆中表现的情况如下

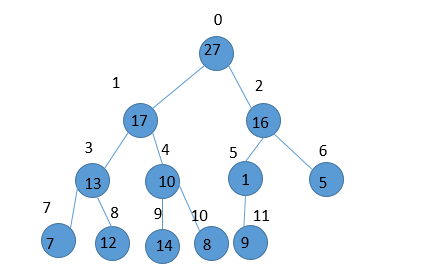
1：各结点之间的性质

对于根节点从  0  开始的一个堆，各个结点存在以下关系  

体现在图(2)中

  //计算二叉树的右孩子下标值
    public int findrightChild(int i) {
          return 2*(i+1);
      }
      
      //计算二叉树的左孩子下标值
      public int findLeftChild(int i) {
          return 2*(i+1)-1;
      }
     
     //计算父亲结点的下标值
     public int findParent(int i){
         return (i-1)/2;
     }

 2：什么是最大堆？

 最大堆指的是除了根节点外所有的结点都满足于：根节点的属性值大于孩子结点的属性值。  A[Parent(i)] >= A[i]

 3：如何进行堆排序？

堆排序之前都必须做下面三种操作：

3.1   MaxHeapify()  

　　用于维持最大堆的性质   时间复杂度为   O(nlogn)     每次都是在破坏的那个元素开始维持性质  并且是自顶向底开始进行的

伪代码描述：

Max_Heap(A,i)
    l = findleftChild(i)
    r = findrightChild(i)
    if l <= A.headSize && A[l] > A[i]
        largest = l
    else largest = i
    if r <= A.headSize && A[r] > A[largest]
        largest = r
    if largest != i
        exchange A[i] with  A[largest]
        Max_Heap(A, largest)

在程序的每一步中，从A[i]、A[LEFT(i)]和A[RIGHT(i)]中选出最大的，并将其下标存储在largest中。如果A[i]是最大的，那么以 i 为根结点的子树已经是最大堆，程序结束。

否则，最大元素是i的某个孩子结点，则交换A[i]和A[largest]的值。从而使i及其孩子都满足最大堆的性质。在交换后，下标为largtst的结点的值是原来的A[i]，于是以该结点为根的子树又有可能会违反最大堆的性质．因此，需要对该子树递归调用MAX-HEAPIFY。

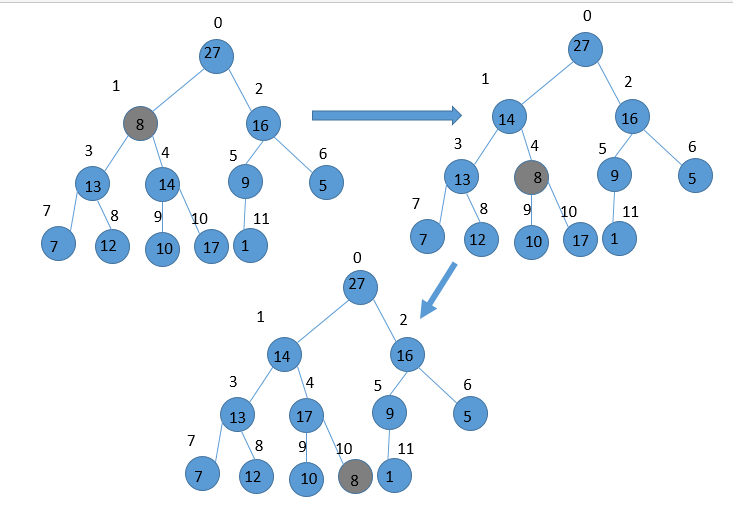
 (1) 首先A[1]违反了最大堆的性质    所以将A[1]与其孩子中更大的一个值作交换，此时    A [1] exchange  A[4]   

（2）A[4]因此不满足最大堆的性质，在继续与其孩子中的更大一个值做交换   

（3）已经到了叶子结点，没有任何的孩子结点，则调出递归的过程

该过程的时间复杂度为  O(n)

3.2  BuildMaxHeap()    

　　创建最大堆    具有线性时间复杂度

思路主要是从低向上的方式将A数组转化为  最大堆的形式

建立堆的伪代码描述：

Create_heap(A)
A.heapSize = A.length;
for i = [A.length/2] downto 1
    Max_Heap(A,i)

 思考：  建立堆的时候为什么  i = [A.length/2]    开始呢？

　　当用数组表示存储n个元素的堆时，叶结点下标分别是[n/2]+1,[n/2]+2,[n/2]+3 ...，n

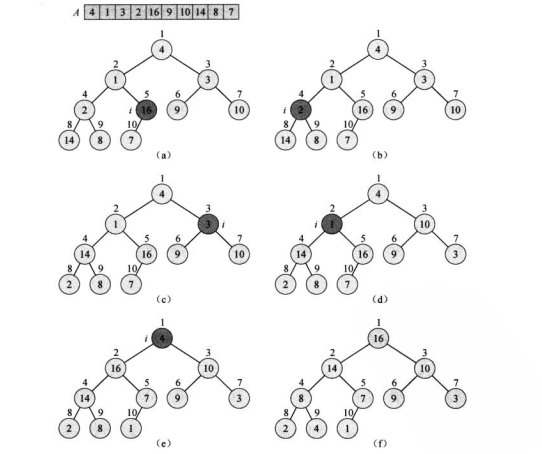
     由上面的图解值，首先从i = length / 2  开始  使每个结点的子树都满足  最大堆的性质。不断的递归调用MaxHeapify() 方法由低向顶部一步一步实现。

3.3  HeapSort()        

　　 对于一个数组做原址排序(原址排序：任何时候只需要常数个的额外空间来保存临时变量)

最后一步：对于已经排列好的堆 ，我们只需要每次将最后一个结点与根节点作交换，并且取出根节点  ，作为输出元素，然后将剩余的结点再调用  MaxHeapify()  方法，让其他结点仍然具有最大堆 的性质。

// (自底向上进行)
HeapSort(A)
    Create_heap(A)
    for i = A.length downto 2
        Exchange A[i] with A[1]
        A.heapSize--
        Max_Heap(A,i)

HEAPSORT过程的时间复杂度是O(nlgn),因为每次调用CreateMaxHeap()的时间复杂度是O(n)，而n-1次调用MAXHEAPIFY，每次的时间为O(lgn)。

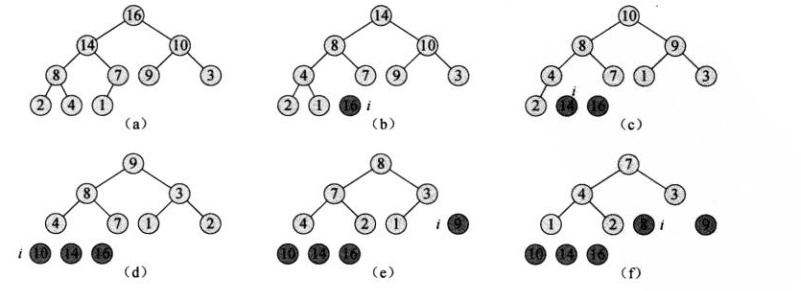
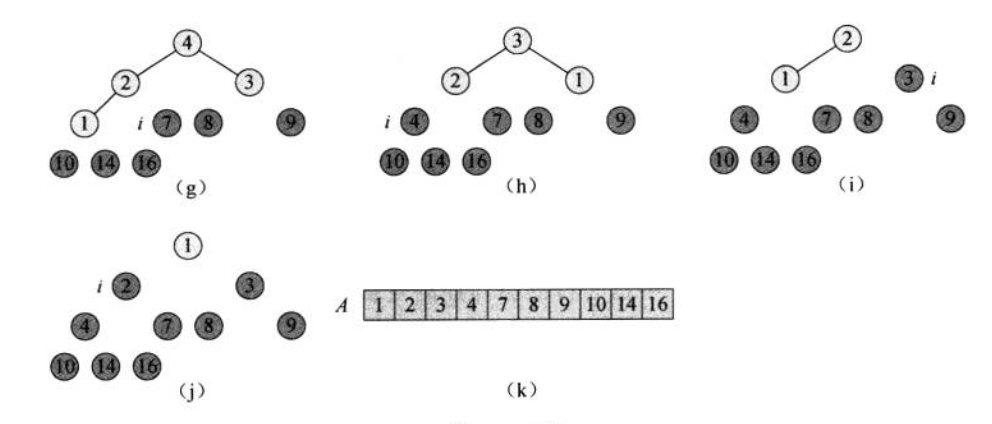
 当所有的元素都递归排序完成，则依次挑出来的元素都为已经排列好的序列。

下面给出具体的实现代码：

package com.hone.heapsort;

public class HeapSort {
    static int[] a = {4,1,3,2,16,9,10,14,8,7};
    public static int [] heap =a ;
    public static int heapsize = heap.length;
    
    //1:保证堆满足最大堆的性质
    /*
     * 这里面的性质有一个问题，对于第一个根节点的元素不是最大值的时候，会出现局部
     * 最大堆  (并不是一个问题，以为每次调用的点，都是从该点开始堆才遭到破坏)
     */
    
    public static  void maxHeap(int[] A , int i){
        
        int largest = i; 
        int l = findLeftChild(i);
        int r = findrightChild(i);
        if (l < heapsize && A[l] > A[i]) 
            largest = l;
        if (r < heapsize && A[r] > A[largest]) 
            largest = r;
        if (largest != i) {
            swap(A,largest,i);
            maxHeap(A, largest);
        }
        
    }
    
    //2:用于创建最大堆
    public  void  createHeap(int[] A){
        for (int i = heapsize/2-1; i >= 0; i--) {
            maxHeap(A, i);
        }
    }

    //3: 用于堆排序算法
    public  void heapSort(int[] A){
        createHeap(A);
        System.out.print("排序后： ");
        for (int i = heapsize-1; i >= 0; i--) {
            swap(A,i,0);
            System.out.print(A[i]+" ");
            heapsize --;
            maxHeap(A, 0);
        }
    }
    
    // 定义一个方法交换两个数据
    private static void swap(int[] a,int i,int j) {
        int temp;
        temp = a[j];
        a[j] = a[i];
        a[i] = temp;
    }
    //定义一个方法计算二叉树的右孩子
    public static int findrightChild(int i) {
        return 2*(i+1);
    }
    
    //定义一个方法计算二叉树的左孩子
    public static int findLeftChild(int i) {
        return 2*(i+1)-1;
    }
    
    
    public static int findParent(int i){
        return (i-1)/2;
    }
    
    public static void main(String[] args){
        HeapSort hs = new HeapSort();
        System.out.print("原数组： ");
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+" ");
        }
        System.out.println();
        hs.heapSort(a);
    }
}

 但是，方法并没有得到完整的封装，而且没有很好的用到java中面向对象的思想。

因此代码做如下改变：

下面代码转载于：http://www.cnblogs.com/developerY/p/3319618.html     只作为学习使用。

package com.hone.heapsort;

//定义一个类将MaxHeap单独的类
public class MaxHeap {
    int[] heap;
    int heapsize;
    
    public MaxHeap(int[] array)
    {
        this.heap=array;    
        this.heapsize=heap.length;
    }
    
    public void BuildMaxHeap()
    {
        for(int i=heapsize/2-1;i>=0;i--)
        {
            Maxify(i);//依次向上将当前子树最大堆化
        }
    }
    
    public void HeapSort()
    {
        for(int i=0;i<heap.length;i++)
        {
            //执行n次，将每个当前最大的值放到堆末尾
            int tmp=heap[0];
            heap[0]=heap[heapsize-1];
            heap[heapsize-1]=tmp;
            heapsize--;
            Maxify(0);
        }
    }
    
    public void Maxify(int i)
    {
        int l=Left(i);
        int r=Right(i);
        int largest;
        
        if(l<heapsize&&heap[l]>heap[i])
            largest=l;
        else
            largest=i;
        if(r<heapsize&&heap[r]>heap[largest])
            largest=r;
        if(largest==i||largest>=heapsize)//如果largest等于i说明i是最大元素 largest超出heap范围说明不存在比i节点大的子女
            return ;
        int tmp=heap[i];//交换i与largest对应的元素位置，在largest位置递归调用maxify
        heap[i]=heap[largest];
        heap[largest]=tmp;
        Maxify(largest);
    }
    
    public void IncreaseValue(int i,int val)
    {
        heap[i]=val;
        if(i>=heapsize||i<=0||heap[i]>=val)
            return;
        int p=Parent(i);
        if(heap[p]>=val)
            return;
        heap[i]=heap[p];
        IncreaseValue(p, val);
    }
    
    private int Parent(int i)
    {
        return (i-1)/2;
    }
    private int Left(int i)
    {
        return 2*(i+1)-1;
    }
    private int Right(int i)
    {
        return 2*(i+1);
    }
}

package com.hone.heapsort;

public class Demo {
    
    public static void main(String[] args)
    {
        int[] array=new int[]{1,2,19,4,7,8,9,10,14,16};
        MaxHeap heap=new MaxHeap(array);
        System.out.println("执行最大堆化前堆的结构：");
        printHeapTree(heap.heap);
        heap.BuildMaxHeap();
        System.out.println("执行最大堆化后堆的结构：");
        printHeapTree(heap.heap);
        heap.HeapSort();
        System.out.println("执行堆排序后数组的内容");
        printHeap(heap.heap);
        
    }
    private static void printHeapTree(int[] array)
    {
        for(int i=1;i<array.length;i=i*2)
        {
            for(int k=i-1;k<2*(i)-1 &&k<array.length;k++)
            {
                System.out.print(array[k]+" ");
            }
            System.out.println();
        }    
    }
    private static void printHeap(int[] array)
    {
        for(int i=0;i<array.length;i++)
        {
            System.out.print(array[i]+" ");
        }
    }
}