主要参考资料 : 算法导论
1:时间复杂度介绍
对于包含n个数的输入数组来说,快速排序是一种最坏情况时间复杂度为O(n2)的排序算法.虽然最坏情况时间复杂度很差,但是快速排序通常是实际排序应用中最好的选择,因为它的平均性能非常好:它的期望时间复杂度是O(nlgn).而且O(nlgn)中隐含的常数因子非常小。另外,它还能够进行原址排序,甚至在虚存环境中也能很好地工作。
2:基本思路
(1)分解:
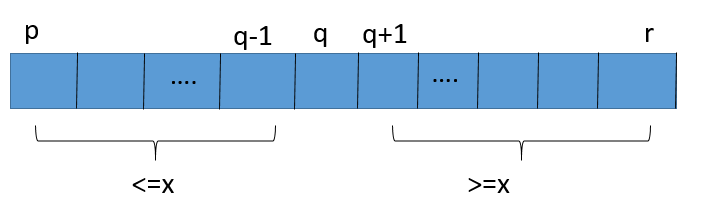
数组A[p ... r]被划分为两个(可能为空)子数组A[p...q-l]和A[q+1 ... r],使得A[p ... q-l]中的每一个元素都小于等于A[q]
而A[q]也小于等于A[q+1...r]中的每个元素。其中,计算下标 q 也是划分过程的一部分。
(2)解决:通过递归调用快速排序,对子数组A[p ... q-l]和A[q+1...r] 进行排序.
(3)合并:因为子数组都是原址排序的,所以不需要合并操作:数组A[p...r]已经有序.
下面给出快速排序的核心代码分析:
如何实现上面的数组划分过程:
1 //定义函数用于主要的划分 p表示数组的下标,r表示数组的上标 2 public int partition(int[] a ,int p, int r){ 3 int x = a[r]; 4 int i = p-1; 5 for (int j = p; j <= r-1; j++) { 6 if (a[j] <= x) { 7 i++; 8 swap(a,i,j); 9 } 10 } 11 swap(a, i+1, r); 12 return i+1; 13 }
下面分析如何对数组进行划分:
(1)首先选择一个 x = A[r] 元素作为主元 (或者“哨兵”)围绕该元素进行划分数组。小于x 放在一起,大于 x 的放在一起。
(2)对于5-10行 循环体的每一轮迭代开始时,对于任意教组下标k,有:
1.若 p ≤ k ≤ i,则A[k] ≤ x。
2.若 i+1 ≤ k ≤ j-l,则A[k ] > x。
3.若 k = r,则 A[k] = x。
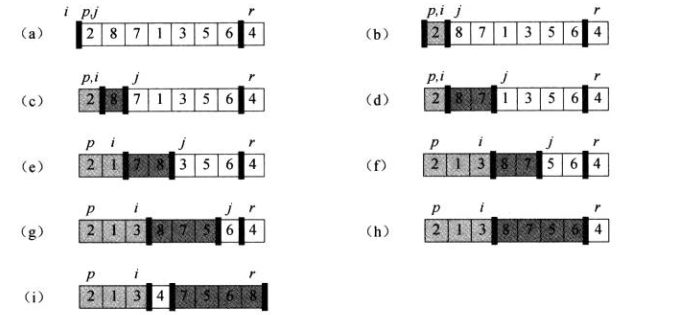
上图表示PARTITION操作过程.数组项A[r]是主元x。浅阴影部分的数组元素都在划分的第一部分,其值都不大于x
深阴影部分的元素都在划分的第二部分,其值都大于x.无阴影的元素则是还未分人这两个部分中的任意一个。最后的白色元素就是主元x。
(a)初始的数组和变最设置.数组元素均未被放人前两个部分中的任何一个.
(b) 2与它自身进行交换,并被放入了元素值较小的那个部分。
(c)~(d)8和7被添加到元素值较大的那个部分中.
(e)l和8进行交换,数值较小的部分规模增加.
(f)数值3和7进行交换,数值较小的部分规模增加.
(g)~(h)5和6被包含进较大部分,循环结束.
(i)在第7~8行中,主元被交换,这样主元就位于两个部分之间
然后分别递归调用 quickSort(A , p, q-1 ) 以及 quickSort(A , q+1, r)
具体的代码实现如下:
1 package com.hone.heapsort; 2 3 4 public class QucikSort { 5 6 //这里面使用一个变量q怎么解决执行第一个递归的时候造成的q值的变化,不在 7 //等于第一次返回的中值 8 public void quickSort(int[] A,int m,int n){ 9 if(m < n){ 10 int q = partition(A, m, n); 11 quickSort(A, m, q-1); 12 quickSort(A, q+1, n); 13 } 14 } 15 16 17 //定义函数用于主要的划分 p表示数组的下标,r表示数组的上标 18 public int partition(int[] a ,int p, int r){ 19 int x = a[r]; 20 int i = p-1; 21 for (int j = p; j <= r-1; j++) { 22 if (a[j] <= x) { 23 i++; 24 swap(a,i,j); 25 } 26 } 27 swap(a, i+1, r); 28 return i+1; 29 } 30 31 private void swap(int[] a, int i, int j) { 32 int temp = a[j]; 33 a[j] = a[i]; 34 a[i] = temp; 35 } 36 37 public void printMy(int[] a){ 38 for (int i = 0; i < a.length; i++) 39 System.out.print(a[i]+" "); 40 System.out.println(); 41 } 42 43 public static void main(String[] args) { 44 int[] a = {2,8,7,1,3,5,6,4}; 45 int m = 0; 46 int n = a.length-1; 47 QucikSort qsort = new QucikSort(); 48 System.out.print("原数组: "); 49 qsort.printMy(a); 50 qsort.quickSort(a, m, n); 51 System.out.print("排序后: "); 52 qsort.printMy(a); 53 } 54 }
4:时间复杂度分析:
最坏情况:当每次划分都产生 n-1 个元素 以及 0个元素的时候,最坏情况就产生了。
T(n) = T(n-1)+T(0)+O(n)
也就是说,如果算法每次递归一次的时候都产生极大的不平衡性,则算法的最坏情况就产生了,并且时间复杂度为 O(n2)。
最好情况:在可能的最平衡的划分中,PARTITION得到的两个子问题的规模都不大于n/2。在这种情况下,快速排序的性能非常好.此时,算法运行时间的递归式为:
T(n) = 2T(n/2)+O(n)
在上式中,可以得到时间复杂度为 O(nlogn)
并且在一般情况下,之后每次二分的比例为常数倍,算法的时间复杂度总是为 O(nlogn)