Labeled Tree: 每个节点都有标号的树,如图1(a)。
Unlabeled Tree: 节点没有标号的树,如图1(b)。
Cayley' Tree Formula: There are $n^{n-2}$ distinct labeled trees of order n.
Prufer's Method:a labeled tree of order n is one-to-one correspondence with a sequence of length n-2.
Prufer's Method 能够帮助我们更简单地证明 Cayley's Tree Formula。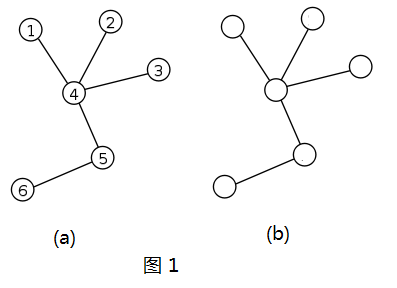
Algorithm 1:Labeled Tree $\rightarrow$ Sequence:
Given: A labeled tree T
- $i=0$, $T_0=T$
- 在 $T_i$ 中找到一个标号值最小的节点,记为 $v$, $u$ 是 $v$ 的邻居.
- Record $u$ in the sequence.
- $T_{i+1}=T_i - \{v\}$.
- If $T_{i+1}=K_2$, then stop. Otherwise, $i=i+1$ and go to step 2.
Algorithm 2:Sequence $\rightarrow$ Labeled tree:
Given: A sequence $\sigma=a_1,a_2,\cdots,a_k$,且每个元素都属于集合$\{1,\cdots,k+2\}$.
- Draw $k+2$ vertices; labeled $v_1,v_2,\cdots,v_{k+2}$. Let $S=\{1,2,\cdots,k+2\}$.
- $i=0,\sigma_0=\sigma,S_0=S$.
- Let $j$ be the smallest number in $S_i$ that does not appear in the sequence $\sigma_i$.
- Let $\sigma_i[1]$ be the first element in $\sigma_i$, add the edge $\{\sigma_i[1],j\}$ to the graph.
- Remove the first element in $\sigma_i$ to create the new sequence $\sigma_{i+1}$. Remove $j$ from $S_i$ to create a new set $S_{i+1}$.
- If $\sigma_{i+1}$ is empty, then the $S_{i+1}$ has only two elements called $a$ and $b$, add an edge $\{a,b\}$, then stop. Otherwise $i=i+1$ and go to step 3.
The correctness of Cayley's Tree Formula :
定理1:Algorithm 1 是 Algorithm 2 的逆过程,通俗地说,给定一棵 Labeled tree T, 你能够通过"Algorithm 1"返回一个序列 $\sigma$,你也一定能够通过"Algorithm 2"将 $\sigma$ 变成树 $T$。
证明:用数学归纳法对节点个数进行归纳。
当 $n=2$ 时,给定一棵树 $K_2$, 通过"Algorithm 1" 获得的sequence为<>(空序列),而将<>通过"Algorithm 2"也会变成 $K_2$,因此成立.
假设 $n=k-1$ 时成立。
当 $n=k$ 时,给定一棵 labeled tree $T$, 设 $i$ 为开始时标号最小的叶子节点,且 $j$ 为与之相邻的点,因此 sequence 的第一个元素为 $j$,且 $i$ 不会出现在 sequence 中,删除节点 $i$ 后,设 $T'=T-\{i\}$,因为 $T'$ 的节点个数为 $k-1$,因此根据归纳假设,$T'$ 能够通过 "Algorithm 1" 返回一个序列 $\sigma'=<\sigma_2,\sigma_3,\cdots,\sigma_{k-2}>$,且通过"Algorithm 2" 变成 $T'$。
因此 $T$ 通过"Algorithm 1" 变成 $\sigma=<j,\sigma_2,\sigma_3,\cdots,\sigma_{k-2}>$,因此现在我们只要证明对 $\sigma$ 运行"Algorithm 2"后,第一个添加的边是 $\{i,j\}$ 即可,这很显然,因为假设第一条边添加的是 $\{k,j\}$,且 $k\neq i$,则将 $T$ 转变成序列时,第一步也应该发现的最小叶子是 $k$,而不是 $i$,因此得证。