二叉排序树

定义

---

• 若左子树非空，则左子树上所有结点关键字值均小于根节点关键字值
• 若右子树非空，则右子树上所有节点关键字值均大于根节点关键字值
• 左，右子树分别是一颗二叉排序树

二叉排序树插入

---

二查排序树插入定义:若原二叉树为空，则直接插入节点。否则，若关键字K小于根节点关键字，则插入到左子树中。若关键字K大于根节点关键字，则插入到右子树当中。插入的时间复杂度是树高O(H)

public void insert(Node p, int k) {
        if (p != null) {
            if (k < p.val)
                if (p.LChild == null) {
                    p.LChild = new Node();
                    p.LChild.val = k;
                } else
                    insert(p.LChild, k);
            else {
                if (p.RChild == null) {
                    p.RChild = new Node();
                    p.RChild.val = k;
                } else
                    insert(p.RChild, k);
            }
        }
}

二叉排序树的删除

---

删除分三种情况：

• 如果被删除的节点是叶子节点，就直接删除
• 如果被删除的节点只有左子树或右子树，则将其左子树或右子树代替该节点
• 如果左右子树都存在，那么则将其右子树中序遍历的第一个节点First替换该节点(值替换)，并将First从树中删除
• 删除节点的时间复杂度为O(H)

public void delete(int k) {
        Node parent = new Node();
        parent.LChild = node;
        Node p = node;
        Node t = null;
        // 找出欲删除的节点P
        while (p != null && p.val != k) {
            parent = p;
            if (k < p.val)
                p = p.LChild;
            else
                p = p.RChild;
        }
        // 欲删节点的左右孩子都不为空
        if (p.LChild != null && p.RChild != null) {
            // 找出p的后继节点(中序遍历)
            Node post = inOrderFisrt(p.RChild);
            // 将后继节点值copy给p
            p.val = post.val;
            // 将欲删除的节点修改为post节点
            p = post;
        }
        // 欲删节点的左孩子或右孩子为空
        if (p.LChild == null)
            t = p.RChild;
        else if (p.RChild == null)
            t = p.LChild;
        if (p == parent.LChild)
            parent.LChild = t;
        else
            parent.RChild = t;
    }

中序遍历查找第一个节点

private Node inOrderFisrt(Node t) {
        Node p = null;
        while (t != null) {
            p = t;
            t = t.LChild;
        }
        return p;
    }

二叉排序树构造

---

在构造二查排序树时，只需要不断调用二叉排序树的插入算法即可。下面的代码是不断从一个数组中取出欲插入的数，然后调用insert方法将其插入到二叉树当中。

private void initBST(Node node, int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            insert(node, arr[i]);
        }
    }

二叉排序树的查找

---

查找算法用递归实现，每次查找时都与根节点进行比较，如果小于根节点，则往左子树上走。否则，向右子树上走。

public Node search(Node p, int k) {
        if (p != null) {
            if (p.val == k)
                return p;
            else {
                if (k > p.val)
                    return search(p.RChild, k);
                else
                    return search(p.LChild, k);
            }
        } else
            return null;
    }

查找效率分析

---

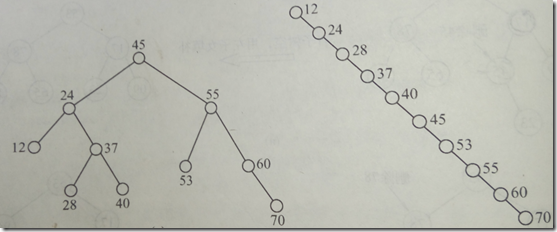
二叉排序树的查找效率和树的构造有关。如果树的左右子树高度相当，那么查找效率为O(logN),否则效率就很低，最低为O(N)。列如下面两棵树，同样找节点70，则左边的效率明显比右边的高。