本文介绍部分主要参考自一博文及《算法导论》。
散列表(Hash Table)是实现字典操作的一种有效数据结构。尽管最坏情况下,散列表中查找一个元素的时间与链表中查找的时间相同,达到了O(n)。然而在实际应用中,散列表的性能是极好的。在一些合理的假设下,在散列表中查找一个元素的平均时间是O(1)。
散列表是普通数组概念的推广。由于对普通数组可以直接寻址,使得能在O(1)时间内访问数组中的任意位置。如果存储空间允许,我们可以提供一个数组,为每个可能的关键字保留一个位置,以利用直接寻址技术的优势。
当实际存储的关键字数目比全部的可能关键字总数要小时,采用散列表就成为直接数组寻址的一种有效替代,因为散列表使用一个长度与实际存储的关键字数目成比例的数组来存储。在散列表中,不是直接把关键字作为数组的下标,而是根据关键字计算出相应的下标。在《算法导论》中,作者介绍了“链接法”和“开放寻址法”来解决关键字“冲突”。其中“冲突”指的是多个关键字映射到数组的同一个下标。
1、直接寻址表
当关键字的的全域(范围)U比较小的时,直接寻址是简单有效的技术,一般可以采用数组实现直接寻址表,数组下标对应的就是关键字的值,即具有关键字k的元素被放在直接寻址表的槽k中。直接寻址表的字典操作实现比较简单,直接操作数组即可以,只需O(1)的时间。
2、散列表
直接寻址表的不足之处在于当关键字的范围U很大时,在计算机内存容量的限制下,构造一个存储|U|大小的表不太实际。当存储在字典中的关键字集合K比所有可能的关键字域U要小的多时,散列表需要的存储空间要比直接寻址表少的很多。散列表通过散列函数h计算出关键字k在槽的位置。散列函数h将关键字域U映射到散列表T[0....m-1]的槽位上。即h:U->{0,1...,m-1}。采用散列函数的目的在于缩小需要处理的小标范围,从而降低了空间的开销。
散列表存在的问题:两个关键字可能映射到同一个槽上,即碰撞(collision)。需要找到有效的办法来解决碰撞。
3、散列函数
好的散列函数的特点是每个关键字都等可能的散列到m个槽位上的任何一个中去,并与其他的关键字已被散列到哪一个槽位无关。多数散列函数都是假定关键字域为自然数N={0,1,2,....},如果给的关键字不是自然数,则必须有一种方法将它们解释为自然数。例如对关键字为字符串时,可以通过将字符串中每个字符的ASCII码相加,转换为自然数。书中介绍了三种设计方案:除法散列法、乘法散法和全域散列法。
3.1 除法散列法
通过取k除以m的余数,将关键字k映射到m个槽的某一个中去。散列函数为:h(k)=k mod m 。m不应是2的幂,通常m的值是与2的整数幂不太接近的质数。
3.2 乘法散列法
这个方法看的时候不是很明白,没有搞清楚什么意思,先将基本的思想记录下来,日后好好消化一下。乘法散列法构造散列函数需要两个步骤。第一步,用关键字k乘上常数A(0<A<1),并抽取kA的小数部分。然后,用m乘以这个值,再取结果的底。散列函数如下:h(k) = m(kA mod 1)。
3.3 全域散列
给定一组散列函数H,每次进行散列时候从H中随机的选择一个散列函数h,使得h独立于要存储的关键字。全域散列函数类的平均性能是比较好的。
4、碰撞处理
通常有两类方法处理碰撞:开放寻址(Open Addressing)法和链接(Chaining)法。前者是将所有结点均存放在散列表T[0..m-1]中;后者通常是把散列到同一槽中的所有元素放在一个链表中,而将此链表的头指针放在散列表T[0..m-1]中。
4.1 开放寻址法
所有的元素都在散列表中,每一个表项或包含动态集合的一个元素,或包含NIL。这种方法中散列表可能被填满,以致于不能插入任何新的元素。在开放寻址法中,当要插入一个元素时,可以连续地检查或探测散列表的各项,直到有一个空槽来放置待插入的关键字为止。有三种技术用于开放寻址法:线性探测、二次探测以及双重探测。
4.1.1 线性探测
给定一个普通的散列函数h':U —>{0,1,.....,m-1},线性探测方法采用的散列函数为:h(k,i) = (h'(k)+i)mod m,i=0,1,....,m-1
探测时从i=0开始,首先探查T[h'(k)],然后依次探测T[h'(k)+1],…,直到T[h'(k)+m-1],此后又循环到T[0],T[1],…,直到探测到T[h'(k)-1]为止。探测过程终止于三种情况:
1)若当前探测的单元为空,则表示查找失败(若是插入则将key写入其中);
2)若当前探测的单元中含有key,则查找成功,但对于插入意味着失败;
3)若探测到T[h'(k)-1]时仍未发现空单元也未找到key,则无论是查找还是插入均意味着失败(此时表满)。
线性探测方法较容易实现,但是存在一次群集问题,即连续被占用的槽的序列变的越来越长。采用例子进行说明线性探测过程,已知一组关键字为(26,36,41,38,44,15,68,12,6,51),用除余法构造散列函数,初始情况如下图所示:

散列过程如下图所示:

4.1.2 二次探测
二次探测法的探查序列是:h(k,i) =(h'(k)+i*i)%m ,0≤i≤m-1 。初次的探测位置为T[h'(k)],后序的探测位置在次基础上加一个偏移量,该偏移量以二次的方式依赖于i。该方法的缺陷是不易探查到整个散列空间。
4.1.3 双重散列
该方法是开放寻址的最好方法之一,因为其产生的排列具有随机选择的排列的许多特性。采用的散列函数为:h(k,i)=(h1(k)+ih2(k)) mod m。其中h1和h2为辅助散列函数。初始探测位置为T[h1(k)],后续的探测位置在此基础上加上偏移量h2(k)模m。
4.2 链接法
将所有关键字为同义词的结点链接在同一个链表中。若选定的散列表长度为m,则可将散列表定义为一个由m个头指针组成的指针数组T[0..m-1]。凡是散列地址为i的结点,均插入到以T[i]为头指针的单链表中。T中各分量的初值均应为空指针。在拉链法中,装填因子α可以大于1,但一般均取α≤1。
举例说明链接法的执行过程,设有一组关键字为(26,36,41,38,44,15,68,12,6,51),用除余法构造散列函数,初始情况如下图所示:
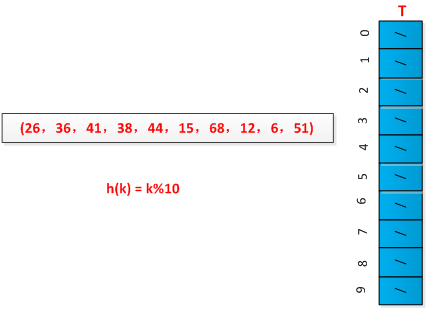
最终结果如下图所示:

关于“链接法”实现的源代码就单元测试代码如下:

1 #ifndef HASHTABLE_H 2 #define HASHTABLE_H 3 4 typedef int Key; 5 typedef int Value; 6 class Node_HT 7 { 8 public: 9 Key key; 10 Value val; 11 Node_HT * pre; 12 Node_HT * post; 13 }; 14 typedef Node_HT * NodePointer_HT; 15 16 const int MAXLEN = 10; 17 18 class HashTable 19 { 20 public: 21 HashTable(); 22 HashTable(Key * key, Value * val, int initLen); 23 virtual ~HashTable(); 24 HashTable(const HashTable & orig); 25 HashTable& operator=(const HashTable & orig); 26 virtual void initST(Key * key, Value * val, int initLen); 27 virtual bool insert(Key key, Value val); 28 virtual bool erase(Key key); 29 virtual Value search(Key key); 30 31 private: 32 NodePointer_HT node[MAXLEN]; 33 int hashFunc(Key key); 34 35 }; 36 37 #endif

1 #include "HashTable.h" 2 #include <iostream> 3 using namespace std; 4 5 HashTable::HashTable() 6 { 7 for (int i = 0; i < MAXLEN; i++) 8 { 9 NodePointer_HT temp = new Node_HT; 10 temp->pre = nullptr; 11 temp->post = nullptr; 12 node[i] = temp; 13 } 14 } 15 16 HashTable::HashTable(Key * key, Value * val, int initLen) 17 { 18 for (int i = 0; i < MAXLEN; i++) 19 { 20 NodePointer_HT temp = new Node_HT; 21 temp->pre = nullptr; 22 temp->post = nullptr; 23 node[i] = temp; 24 } 25 for (int i = 0; i < initLen; i++) 26 { 27 insert(key[i], val[i]); 28 } 29 } 30 31 HashTable::~HashTable() 32 { 33 for (int i = 0; i < MAXLEN; i++) 34 { 35 NodePointer_HT ptr = node[i]; 36 NodePointer_HT temp; 37 while (ptr != nullptr) 38 { 39 temp = ptr->post; 40 delete ptr; 41 ptr = temp; 42 } 43 } 44 } 45 46 HashTable::HashTable(const HashTable & orig) 47 { 48 // leave blank 49 } 50 51 HashTable& HashTable::operator=(const HashTable & orig) 52 { 53 // leave blank 54 return *this; 55 } 56 57 void HashTable::initST(Key * key, Value * val, int initLen) 58 { 59 for (int i = 0; i < initLen; i++) 60 { 61 insert(key[i], val[i]); 62 } 63 } 64 65 bool HashTable::insert(Key key, Value val) 66 { 67 int pos = hashFunc(key); 68 NodePointer_HT temp = new Node_HT; 69 temp->key = key; 70 temp->val = val; 71 72 if (node[pos] == nullptr) 73 { 74 NodePointer_HT ptr = node[pos]->post; 75 ptr = temp; 76 temp->pre = ptr; 77 temp->post = nullptr; 78 } 79 else 80 { 81 NodePointer_HT ptr = node[pos]; 82 NodePointer_HT parentPtr; 83 while (ptr != nullptr) 84 { 85 if (ptr->key == key) 86 { 87 cout << "There has been a repeated key " << key << "in " << pos << "th slot!" << endl; 88 return false; 89 } 90 parentPtr = ptr; 91 ptr = ptr->post; 92 } 93 94 parentPtr->post = temp; 95 temp->pre = parentPtr; 96 temp->post = nullptr; 97 } 98 99 return true; 100 } 101 102 bool HashTable::erase(Key key) 103 { 104 bool isFind = false; 105 106 int pos = hashFunc(key); 107 NodePointer_HT ptr = node[pos]->post; 108 while (ptr != nullptr) 109 { 110 if (ptr->key == key) 111 { 112 NodePointer_HT prePtr; 113 NodePointer_HT postPtr; 114 if (ptr->post != nullptr) 115 { 116 prePtr = ptr->pre; 117 postPtr = ptr->post; 118 prePtr->post = postPtr; 119 postPtr->pre = prePtr; 120 } 121 else 122 { 123 prePtr = ptr->pre; 124 prePtr->post = nullptr; 125 } 126 127 isFind = true; 128 delete ptr; 129 break; 130 } 131 132 ptr = ptr->post; 133 } 134 135 return isFind; 136 } 137 138 Value HashTable::search(Key key) 139 { 140 Value val = NULL; 141 142 int pos = hashFunc(key); 143 NodePointer_HT ptr = node[pos]->post; 144 while (ptr != nullptr) 145 { 146 if (ptr->key == key) 147 { 148 val = ptr->val; 149 break; 150 } 151 ptr = ptr->post; 152 } 153 154 return val; 155 } 156 157 int HashTable::hashFunc(Key key) 158 { 159 return key % 10; 160 }

1 #include "stdafx.h" 2 #include "CppUnitTest.h" 3 #include "../Searching/HashTable.h" 4 5 using namespace Microsoft::VisualStudio::CppUnitTestFramework; 6 7 namespace HashTableUT_Namespace 8 { 9 TEST_CLASS(HashTableUT) 10 { 11 public: 12 HashTableUT() 13 { 14 testHT = new HashTable; 15 } 16 17 ~HashTableUT() 18 { 19 delete testHT; 20 } 21 22 TEST_METHOD(HashTable_Normal_Test) 23 { 24 int key[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19}; 25 int val[] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19}; 26 int len = sizeof(key) / sizeof(int); 27 28 testHT->initST(key, val, len); 29 30 bool expect, actual; 31 expect = true; 32 actual = testHT->erase(14); 33 Assert::AreEqual(expect, actual); 34 35 expect = true; 36 actual = testHT->erase(4); 37 Assert::AreEqual(expect, actual); 38 39 expect = false; 40 actual = testHT->erase(100); 41 Assert::AreEqual(expect, actual); 42 43 Value expectVal, actualVal; 44 expectVal = 5; 45 actualVal = testHT->search(5); 46 Assert::AreEqual(expectVal, actualVal); 47 48 expectVal = NULL; 49 actualVal = testHT->search(4); 50 Assert::AreEqual(expectVal, actualVal); 51 } 52 53 public: 54 HashTable * testHT; 55 56 }; 57 }
代码已托管至Github.
