Description:
Count the number of prime numbers less than a non-negative number, n.
求0-n的素数个数,使用埃拉托斯特尼筛法
要得到自然数n以内的全部素数,必须把不大于 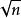 的所有素数的倍数剔除,剩下的就是素数。
的所有素数的倍数剔除,剩下的就是素数。
给出要筛数值的范围n,找出以内的素数。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个质数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个质数5筛,把5留下,把5的倍数剔除掉;不断重复下去......。
步骤
详细列出算法如下:
- 列出2以后的所有序列:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 标出序列中的第一个素数,也就是2,序列变成:
- 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
- 将剩下序列中,划掉2的倍数,序列变成:
- 2 3 5 7 9 11 13 15 17 19 21 23 25
- 如果现在这个序列中最大数小于最后一个标出的素数的平方,那么剩下的序列中所有的数都是素数,否则回到第二步。
- 本例中,因为25大于2的平方,我们返回第二步:
- 剩下的序列中第一个素数是3,将主序列中3的倍数划掉,主序列变成:
- 2 3 5 7 11 13 17 19 23 25
- 我们得到的素数有:2,3
- 25仍然大于3的平方,所以我们还要返回第二步:
- 现在序列中第一个素数是5,同样将序列中5的倍数划掉,主序列成了:
- 2 3 5 7 11 13 17 19 23
- 我们得到的素数有:2,3,5 。
- 因为23小于5的平方,跳出循环.
结论:2到25之间的素数是:2 3 5 7 11 13 17 19 23。
class Solution(object):def countPrimes(self, n):""":type n: int:rtype: int"""isPrime = [True] * max(n, 2)isPrime[0], isPrime[1] = False, Falsex = 2while x * x < n:if isPrime[x]:p = x * xwhile p < n:isPrime[p] = Falsep += xx += 1return sum(isPrime)