第二课主要介绍第一课余下的BFPRT算法和第二课部分内容
1、BFPRT算法详解与应用
找到第K小或者第K大的数。
普通做法:先通过堆排序然后取,是n*logn的代价。
// O(N*logK)
public static int[] getMinKNumsByHeap(int[] arr, int k) {
if (k < 1 || k > arr.length) {
return arr;
}
int[] kHeap = new int[k];//存放第k小的数
for (int i = 0; i != k; i++) {//把k个数形成大顶堆
heapInsert(kHeap, arr[i], i);
}
//剩余的数,逐个检查是否有小于堆顶的数
for (int i = k; i != arr.length; i++) {
if (arr[i] < kHeap[0]) {
kHeap[0] = arr[i];
heapify(kHeap, 0, k);
}
}
return kHeap;
}
public static void heapInsert(int[] arr, int value, int index) {
arr[index] = value;
while (index != 0) {
int parent = (index - 1) / 2;
if (arr[parent] < arr[index]) {
swap(arr, parent, index);
index = parent;
} else {
break;
}
}
}
public static void heapify(int[] arr, int index, int heapSize) {
int left = index * 2 + 1;
int right = index * 2 + 2;
int largest = index;
while (left < heapSize) {
if (arr[left] > arr[index]) {
largest = left;
}
if (right < heapSize && arr[right] > arr[largest]) {
largest = right;
}
if (largest != index) {
swap(arr, largest, index);
} else {
break;
}
index = largest;
left = index * 2 + 1;
right = index * 2 + 2;
}
}
基于荷兰国旗问题,可以实现o(N)的代价。
每次都分小于等于大于区域,再判断是拿大于区域还是小于区域继续划分,等于的话就直接出答案。
选划分值是关键。最差情况可能导致o(n²)
因为每个位置都是等概率的,概率累加,数学上的长期期望是o(n)的。
BFPRT算法,是严格o(n)的。
流程:
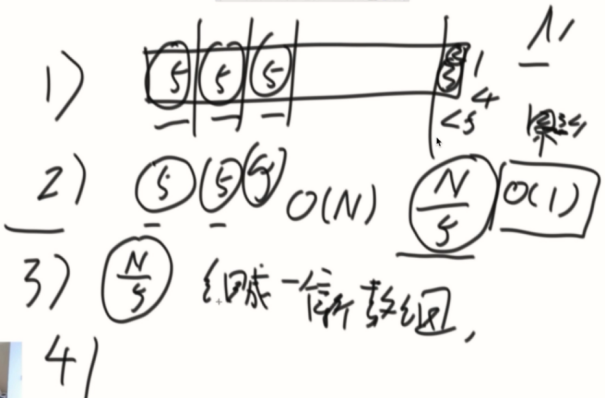
bfprt获得划分的中位数
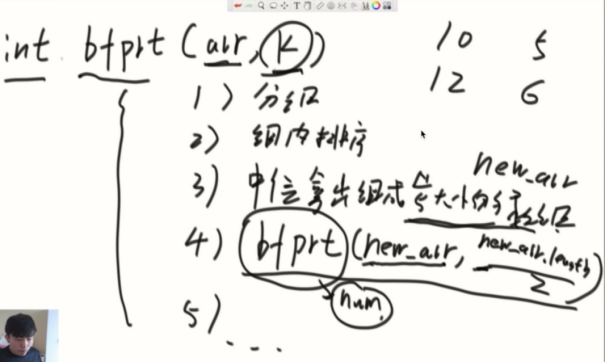
例子:
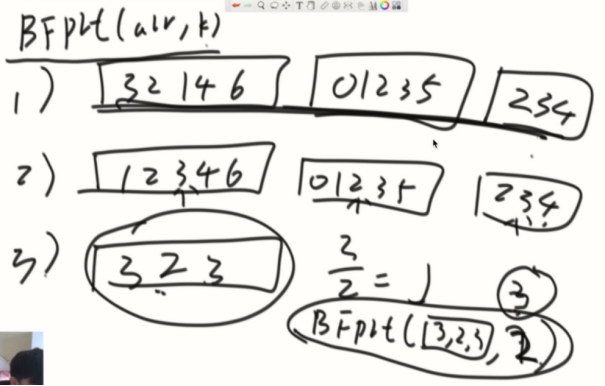
目的:达到第三步如果还超过5个,要继续递归调用划分,直到少于5个找到划分值。
为什么选这个值?
复杂度分析:
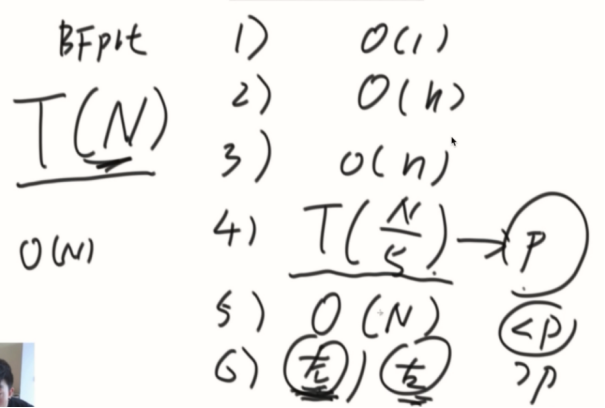
按照最差情况最多多少个数比P要小、最多多少个数比P要大。
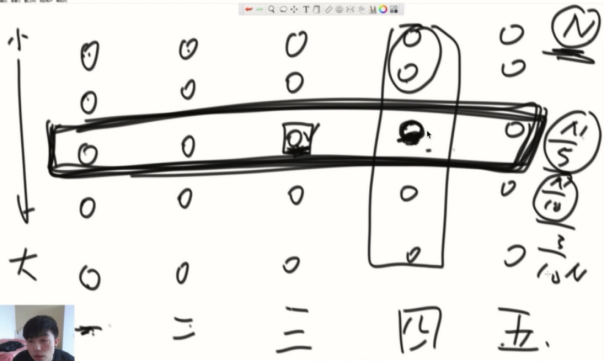
至少有3N/10个比你大。最多7N/10个比你小。
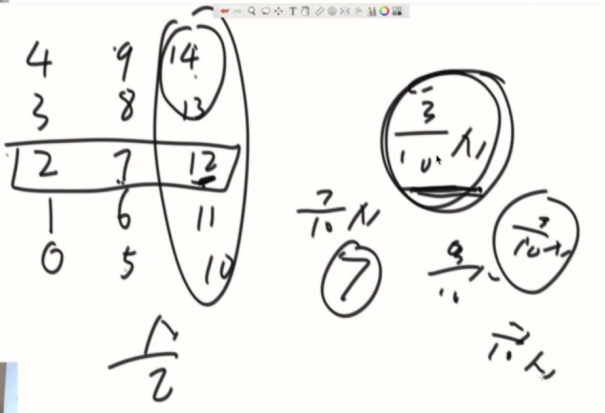
1、逻辑分组
2、组内排序
3、所有数组成一个数组
4、BFPRT调用自己
5、做划分值
6、如果没命中,左右两边只走一侧,左/右部分最多7n/10。
应用:在一个数组中,找出最大/小的K个数的问题。
大部分用堆做o(n*logn),最优解是BFPRT。
// O(N)
public static int[] getMinKNumsByBFPRT(int[] arr, int k) {
if (k < 1 || k > arr.length) {
return arr;
}
//获得第K小的数
int minKth = getMinKthByBFPRT(arr, k);
int[] res = new int[k];//答案数组
int index = 0;
for (int i = 0; i != arr.length; i++) {
if (arr[i] < minKth) {//把小于K的加入到数组
res[index++] = arr[i];
}
}
for (; index != res.length; index++) {//不足补K
res[index] = minKth;
}
return res;
}
public static int getMinKthByBFPRT(int[] arr, int K) {
int[] copyArr = copyArray(arr);
return bfprt(copyArr, 0, copyArr.length - 1, K - 1);
}
public static int[] copyArray(int[] arr) {
int[] res = new int[arr.length];
for (int i = 0; i != res.length; i++) {
res[i] = arr[i];
}
return res;
}
//获得第i小的数
public static int bfprt(int[] arr, int begin, int end, int i) {
if (begin == end) {
return arr[begin];
}
//获得中位数的中位数,作为划分值
int pivot = medianOfMedians(arr, begin, end);
int[] pivotRange = partition(arr, begin, end, pivot);
if (i >= pivotRange[0] && i <= pivotRange[1]) {//命中
return arr[i];
} else if (i < pivotRange[0]) {
return bfprt(arr, begin, pivotRange[0] - 1, i);
} else {
return bfprt(arr, pivotRange[1] + 1, end, i);
}
}
//获得中位数的中位数
public static int medianOfMedians(int[] arr, int begin, int end) {
int num = end - begin + 1;//总数
int offset = num % 5 == 0 ? 0 : 1;//不够五个自成一组
int[] mArr = new int[num / 5 + offset];//中位数组成的数组
for (int i = 0; i < mArr.length; i++) {
int beginI = begin + i * 5;//开始位置
int endI = beginI + 4;
mArr[i] = getMedian(arr, beginI, Math.min(end, endI));
}
//复用bfprt,找出数组中第中间小的数,即中位数。
return bfprt(mArr, 0, mArr.length - 1, mArr.length / 2);
}
public static int[] partition(int[] arr, int begin, int end, int pivotValue) {
int small = begin - 1;
int cur = begin;
int big = end + 1;
while (cur != big) {
if (arr[cur] < pivotValue) {
swap(arr, ++small, cur++);
} else if (arr[cur] > pivotValue) {
swap(arr, cur, --big);
} else {
cur++;
}
}
int[] range = new int[2];
range[0] = small + 1;//等于区域的最左
range[1] = big - 1;//最右
return range;
}
public static int getMedian(int[] arr, int begin, int end) {
insertionSort(arr, begin, end);
int sum = end + begin;
System.out.println(end + " " + begin + " " + sum);
int mid = (sum / 2) + (sum % 2);//取中位数
System.out.println(mid + "----" + arr[mid]);
return arr[mid];
}
public static void insertionSort(int[] arr, int begin, int end) {
for (int i = begin + 1; i != end + 1; i++) {
for (int j = i; j != begin; j--) {
if (arr[j - 1] > arr[j]) {
swap(arr, j - 1, j);
} else {
break;
}
}
}
}
public static void swap(int[] arr, int index1, int index2) {
int tmp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = tmp;
}
public static void printArray(int[] arr) {
for (int i = 0; i != arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
public static void main(String[] args) {
int[] arr = {6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9};
// sorted : { 1, 1, 1, 1, 2, 2, 2, 3, 3, 5, 5, 5, 6, 6, 6, 7, 9, 9, 9 }
printArray(getMinKNumsByHeap(arr, 10));
printArray(getMinKNumsByBFPRT(arr, 10));
}
第二课内容
1、介绍窗口及窗口内最大值或最小值的更新结构(单调双向队列)
双端队列结构。
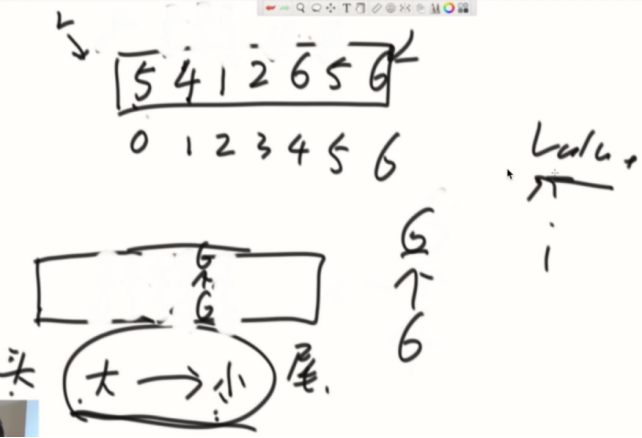
加数逻辑:进来的数如果比他前面的数要大,那就把前面比他小的全部弹出。
减数逻辑:L向前移动,说明某一下标过期,到队列中检查头部节点是否过期,过期就弹出。
队列中留的数,在L缩的时候,都有可能成为最大值。
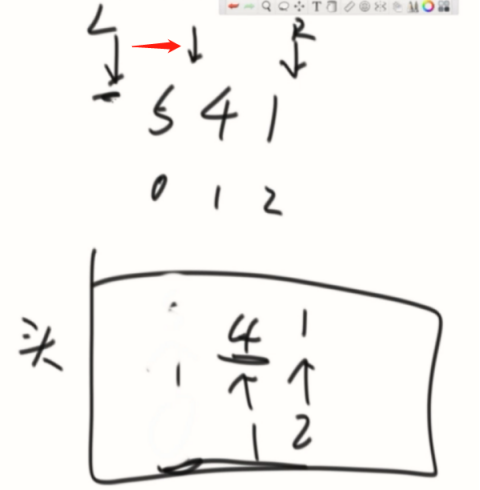
这个情况,3进来干掉了前面进去的1,因为减数是左到右的,1不可能再成为最大值了,所以如果6进来,前面的都可以干掉了。
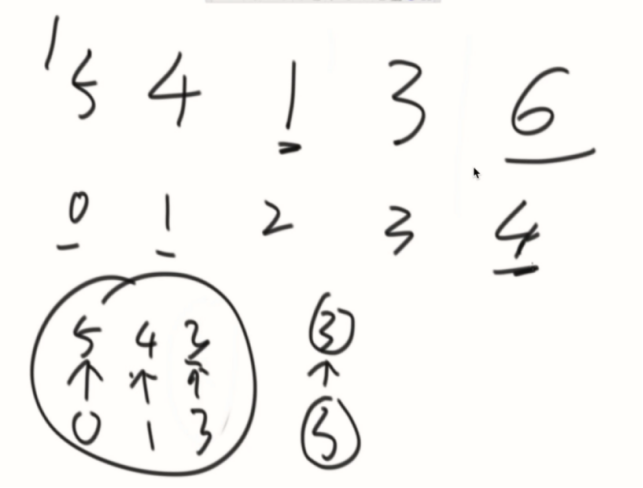
总规则:LR不回退、L不能超过R。
下标必须要,下面的情况以下标大为主。

应用
1、生成窗口最大值数组
有一个整型数组arr和一个大小为w的窗口从数组的最左边滑到最右边,窗口每次向右边滑一个位置。
例如,数组为[4,3,5,4,3,3,6,7],窗口大小为3时:
[4 3 5] 4 3 3 6 7 窗口中最大值为5
4 [3 5 4] 3 3 6 7 窗口中最大值为5
4 3 [5 4 3] 3 6 7 窗口中最大值为5
4 3 5 [4 3 3] 6 7 窗口中最大值为4
4 3 5 4 [3 3 6] 7 窗口中最大值为6
4 3 5 4 3 [3 6 7] 窗口中最大值为7
如果数组长度为n,窗口大小为w,则一共产生n-w+1个窗口的最大值。
请实现一个函数,给定一个数组arr,窗口大小w。
返回一个长度为n-w+1的数组res,res[i]表示每一种窗口状态下的最大值。以本题为例,结果应该返回[5,5,5,4,6,7]。
详见代码...
public class Code_01_SlidingWindowMaxArray {
public static int[] getMaxWindow(int[] arr, int w) {
if(arr == null || w < 1 || arr.length < w){
return null;
}
LinkedList<Integer> qmax = new LinkedList<Integer>();//双向链表,双端队列
int[] res = new int[arr.length - w + 1];
int index = 0;
for (int i = 0; i < arr.length; i++) {
//当队列不是空且入队列的数大于原队列的最后一个数
while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[i]) {
qmax.pollLast();
}
qmax.addLast(i);
//每次加一个,缩一个的时候就看看头节点是否过期。
///当窗口向右移动,原来在窗口中的最左端数字失效了比如1234,w=3,移动到了4,3-3=0,所以下标为0的就失效,退出队列
if(qmax.peekFirst() == i - w){
qmax.pollFirst();
}
//当i大于等于窗口大小时才开始计算窗口里的最大值
if (i >= w - 1) {
res[index++] = arr[qmax.peekFirst()];
}
}
return res;
}
public static void main(String[] args) {
int[] arr={2,3,4,2,6,2,5,1};
int[] maxWindow = getMaxWindow(arr, 3);
for (int i = 0; i < maxWindow.length; i++) {
System.out.print(maxWindow[i]+"-");
}
}
}
2、最大值减去最小值小于或等于num的子数组数量
给定数组arr和整数num,返回有多少个子数组满足如下情况:
max(arr[i..j]) - min(arr[i..j]) <= num
max(arr[i..j])表示子数组arr[i..j]中的最大值,min(arr[i..j])表示子数组arr[i..j]中的最小值。
要求:
如果数组长度为 N,请实现时间复杂度为 O(N)的解法。
子数组的数量。(子数组是连续的)
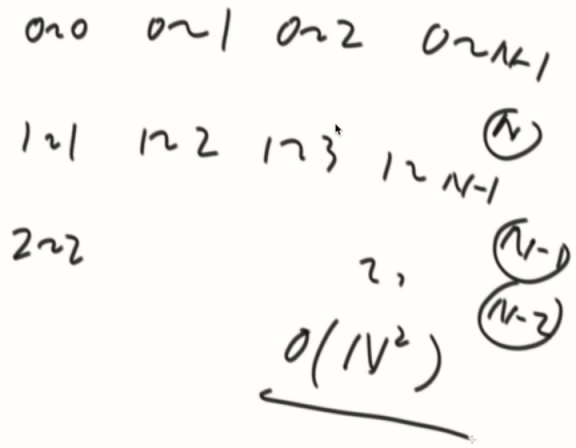
暴力方法o(n^3),没必要看了。

//暴力的方法o(n^3),没必要看了 public static int getNum1(int[] array,int num) { int count = 0; for (int start = 0; start != array.length; start++) { for (int end = start; end != start; end++) { if (isValid(array,start,end,num)) count++; } } return count; } public static boolean isValid(int[] array, int s, int e, int num) { int MAX = Integer.MAX_VALUE; int MIN = Integer.MIN_VALUE; for (int n = s; n != e; n++) {//找出最大最小 MAX = Math.max(array[n], MAX); MIN = Math.min(array[n], MIN); } return MAX - MIN <= num; }
先说几个结论:
1、一个数组L~R达标,内部的子数组一定达标。
缩小范围只可能让MAX变小、MIN变大
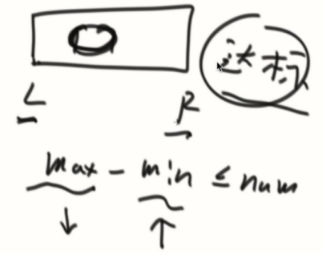
2、L~R不达标,数组往外扩肯定不达标。
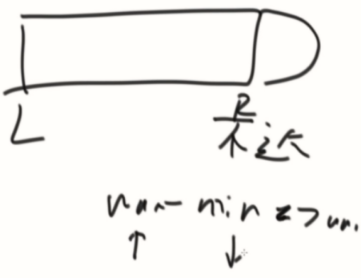
利用这个性质,加上双端队列。
使用窗口最大/小值,在扩充下一个后是不达标的位置停下。
假设是0~X,那么就得到了X+1个以0开头的达标数组。(再往后都是不达标的,所以以0开头的全部找出res += x+1)
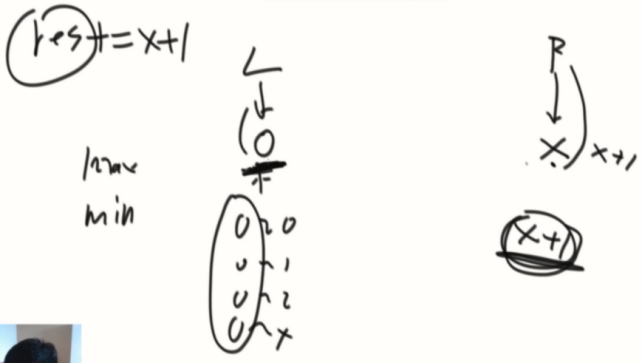
接着,L向前移动,R可以继续向前扩,同理到了不能扩的地方就停,L所在的位置就全部计算出。

public static int getNum(int[] arr, int num) { if (arr == null || arr.length == 0) { return 0; } //准备最大/小值的更新结构 LinkedList<Integer> qmin = new LinkedList<Integer>(); LinkedList<Integer> qmax = new LinkedList<Integer>(); int L = 0; int R = 0; int res = 0; while (L < arr.length) { while (R < arr.length) {//R扩到不能再扩,停 //最小值结构更新 while (!qmin.isEmpty() && arr[qmin.peekLast()] >= arr[R]) { qmin.pollLast(); } qmin.addLast(R); ////最大值结构更新 while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) { qmax.pollLast(); } qmax.addLast(R); //不达标 if (arr[qmax.getFirst()] - arr[qmin.getFirst()] > num) { break; } R++; } //L向前推动,双端队列进行调整 if (qmin.peekFirst() == L) { qmin.pollFirst(); } if (qmax.peekFirst() == L) { qmax.pollFirst(); } res += R - L; L++;//换一个开头 } return res; } public static void main(String[] args) { // TODO Auto-generated method stub int[] arr_test = {1, 2, 3, 4, 5, 6, 7, 8, 9}; int num_test = 4; int res_test; res_test = getNum(arr_test, num_test); System.out.printf("res = %d", res_test); }
3、介绍单调栈结构
在一个数组中,所有的数左/右边距离最近的比他大的数。
能不能o(n)做到
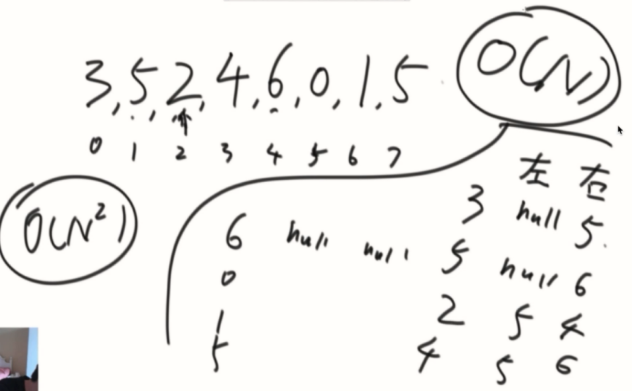
弹出的时候生成信息。
让他弹出的是右边比他大的,他下面的是左边最近比他大的。
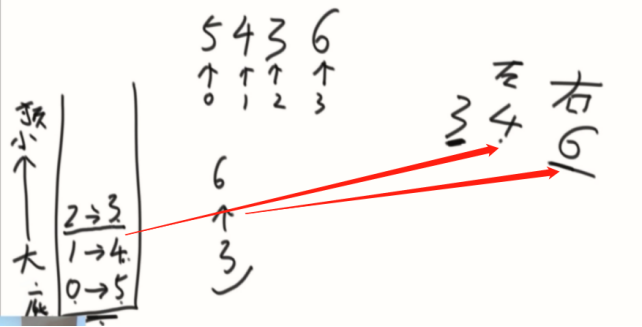
如果数组遍历完,就单独处理栈内的信息。单独弹出的右边为null,左边是底下的数。
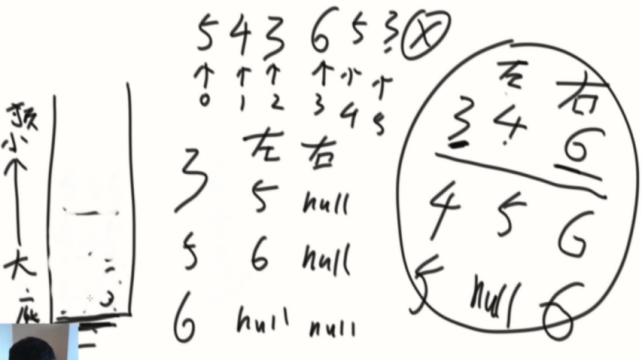
特殊情况:
相同的数,压在一起。
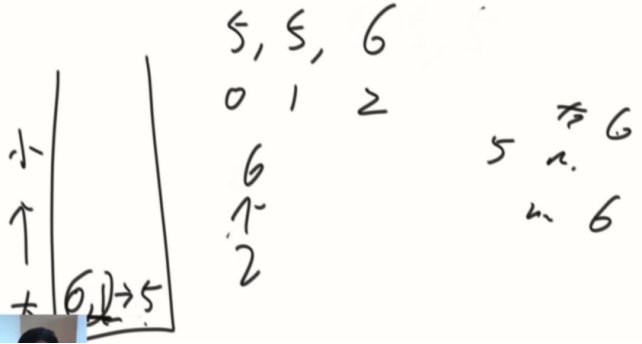
相等情况,不会有影响,下标压在一起,共同结算即可。

这个流程为什么对?
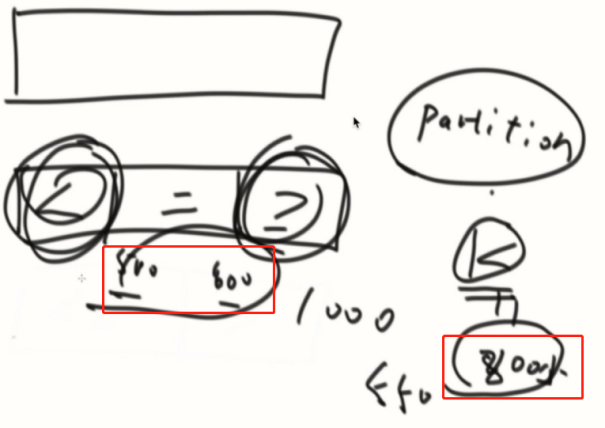
因为我们的逻辑是遇到大的就弹出,所以a在碰到c之前,肯定没有遇到比自己大的数,才会等到c出现才弹出的。
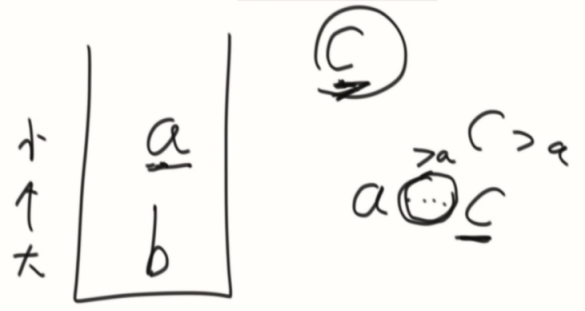
b肯定在a的左边,为什么b在a的下面?肯定是因为b大于a,如果b和a之间存在数,肯定是小于a的,那并不影响我们的查找左边最近大于a的数的逻辑。也不会存在a<x<b的数,存在的话,就轮不到a挨着b了,会变成a x b。
所以流程证明完毕。