动态规划——数塔问题

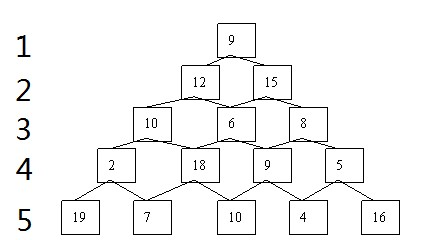
从数塔顶层出发，每个结点可以选择向左走或向右走，要求一直走到塔底，使得走过的路径上的数值和最大。

#include <iostream>
#include <cstdio>
using namespace std;
const int N = 100;
// 下面这个函数实现的是更新最大值，o赋值为o和x的最大值
template <class T>
void updateMax(T& o, const T& x) {
    o = (o > x) ? o : x;
}

// f数组为动态规划的状态数组
// num数组为读入的数塔
// n为读入的数塔高度
int f[N][N], num[N][N], n;

int main() {
    // 读入n和数塔数组num
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= i; ++j) {
            scanf("%d", &num[i][j]);
        }
    }

    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            //从上到下 用另一个数组储存走到当前最大的值
            updateMax(f[i][j],max(f[i - 1][j],f[i - 1][j - 1])+num[i][j]);
        }
    }// step 1 begin: 在这里实现动态规划算法逻辑
    
    // step 1 end.

    // 定义最终结果变量result，因为是计算最大值，所以初始化为0
    int result = 0;
    for (int i = 1; i <= n; ++i) {//因为上一个循环已经计算了值 所以可以直接在最后一层查找
        // step 2 begin: 在这里实现更新最终结果的逻辑
        updateMax(result,f[n][i]);//是赋值而不是交换 记住啦！！！！！！
        // step 2 end.
    }
    // 输出最终最大权值和result
    printf("%d
", result);
    return 0;
}