本篇讲述了在机器学习应用时,如何进行下一步的优化。如训练样本的切分验证?基于交叉验证的参数与特征选择?在训练集与验证集上的学习曲率变化?在高偏差或者高方差时如何进行下一步的优化,增加训练样本是否有效?
更多内容参考 机器学习&深度学习
如果已经创建好了一个机器学习的模型,当我们训练之后发现还存在很大的误差,下一步应该做什么呢?通常能想到的是:
- 1 获取更多的数据
- 2 尝试选择更少的特征集合
- 3 获得更多的特征
- 4 增加多项式特征
- 5 增加λ
- 6 减小λ
样本的切分:首先针对我们的样本集,选择其中的70%作为训练集,训练模型;选择其中的30%作为测试集,验证模型的准确度。当使用交叉验证时,就不能简单的把数据集分成两份了,因为这样无法同时选择模型并衡量模型的好坏。因此可以把样本分成3份,其中60%作为训练集,20%作为交叉验证集,20%作为准确率测试集。

通过多项式的维度与训练集和验证集的误差可以画出上面的图形。如果多项式维度很低,训练集和测试集误差都很大,就叫做高偏差,即欠拟合。如果维度很高,训练集的误差很低,但是验证集误差很高,就叫做高方差,即过拟合。针对正则化λ也可以用这种方式进行选择:

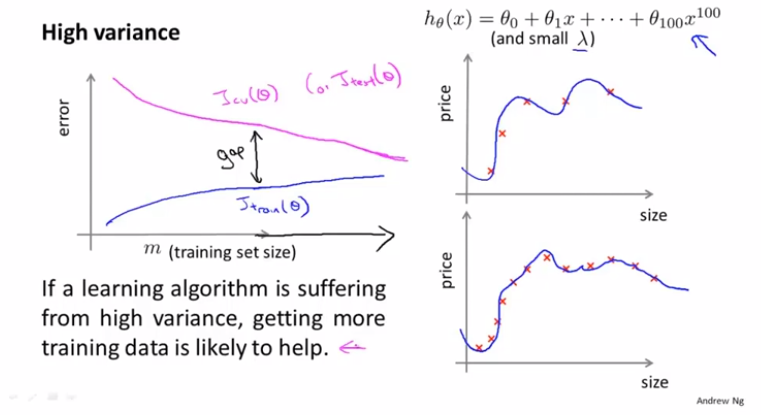
当训练样本很少时,训练的模型在训练集上很容易就拟合出来,所以误差很小,随着训练样本的增加,误差也随之增加;对于验证集,由于最开始的样本很少,泛化能力很差,所以误差很高,随着样本的增加,验证集的效果越来越好。

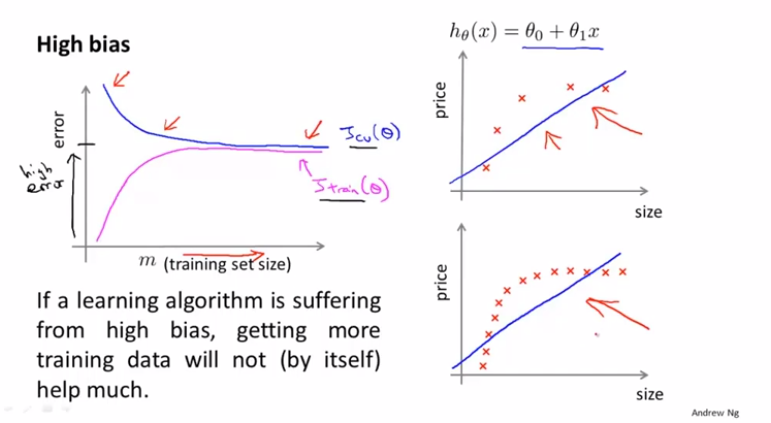
针对于高偏差的情况,由于多项式维度很低,所以拟合出来的是一条直线。因此随着样本的增加,训练集的误差也会增加,但是最后会趋于稳定。此时,增加样本数量并没有什么作用。
针对于高方差的情况,增加样本则会帮助模型拟合的更好。