Codeforces Round #118 (Div. 1) A 矩阵快速幂

A. Plant

 

Dwarfs have planted a very interesting plant, which is a triangle directed "upwards". This plant has an amusing feature. After one year a triangle plant directed "upwards" divides into four triangle plants: three of them will point "upwards" and one will point "downwards". After another year, each triangle plant divides into four triangle plants: three of them will be directed in the same direction as the parent plant, and one of them will be directed in the opposite direction. Then each year the process repeats. The figure below illustrates this process.

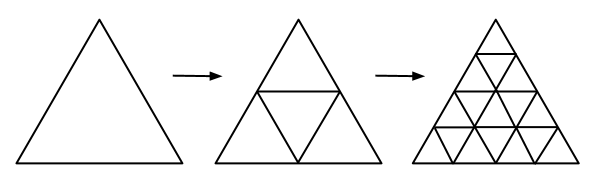
Help the dwarfs find out how many triangle plants that point "upwards" will be in n years.

Input

The first line contains a single integer n (0 ≤ n ≤ 1018) — the number of full years when the plant grew.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use cin, cout streams or the %I64dspecifier.

Output

Print a single integer — the remainder of dividing the number of plants that will point "upwards" in n years by 1000000007 (109 + 7).

Examples

input

Copy

1

output

Copy

3

input

Copy

2

output

Copy

10

Note

The first test sample corresponds to the second triangle on the figure in the statement. The second test sample corresponds to the third one.

一个向上的三角形会变成三个向上的三角形和一个向下的三角形。

一个向下的三角形会变成三个向下的三角形和一个向上的三角形。

设当前有Xn个向上的三角形，Yn个向下的三角形。

那个优

X_n　　　　　　3　　   1　　　X_n-1　

　　　　=

Y_n   　　　　   1　　    3　　   Y_n-1

有公式就好写代码了。

// an = 2*a(n-1)+4^(n-1)
// 设向上的有Xn，向下有Yn
// 那么有：
// Xn = 3*X(n-1) + Y(n-1)
// Yn = X(n-1) + 3*Y(n-1)
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 1000000007;
struct mat{
    ll m[2][2];
    mat(){
        memset(m, 0, sizeof(m));
    }
};

mat mul(mat &A, mat &B) {
    mat C;
    for(int i = 0; i < 2; i++) {
        for(int j = 0; j < 2; j ++) {
            for(int k = 0; k < 2; k ++) {
                C.m[i][j] = (C.m[i][j] + A.m[i][k]*B.m[k][j]) % mod;
            }
        }
    }
    return C;
}

mat pow(mat A, ll n) {
    mat B;
    for(int i = 0; i < 2; i ++) B.m[i][i] = 1;
    while(n) {
        if(n&1) B = mul(B, A);
        A = mul(A, A);
        n >>= 1;
    }
    return B;
}
int main() {
    ll n;
    cin >> n;
    mat A;
    A.m[0][0] = A.m[1][1] = 3;
    A.m[0][1] = A.m[1][0] = 1;
    A = pow(A, n);
    cout << A.m[0][0]<< endl;
    return 0;
}