ACM-ICPC 2015 Changchun Preliminary Contest ABEGHJ

A Alisha's Party

Princess Alisha invites her friends to come to her birthday party. Each of her friends will bring a gift of some value vv, and all of them will come at a different time. Because the lobby is not large enough, Alisha can only let a few people in at a time. She decides to let the person whose gift has the highest value enter first.

Each time when Alisha opens the door, she can decide to let pp people enter her castle. If there are less than pppeople in the lobby, then all of them would enter. And after all of her friends has arrived, Alisha will open the door again and this time every friend who has not entered yet would enter.

If there are two friends who bring gifts of the same value, then the one who comes first should enter first. Given a query nn Please tell Alisha who the nn−th person to enter her castle is.

Input Format

The first line of the input gives the number of test cases, TT, where 1 le T le 151≤T≤15.

In each test case, the first line contains three numbers k, mk, m and qq separated by blanks. kk is the number of her friends invited where 1 le k le 150,0001≤k≤150,000. The door would open mm times before all Alisha's friends arrive where 0 le m le k0≤m≤k. Alisha will have qq queries where 1 le q le 1001≤q≤100.

The ii−th of the following kk lines gives a string B_iBi​, which consists of no more than 200200 English characters, and an integer v_i, 1 le v_i le 10^8vi​, 1≤vi​≤108, separated by a blank. B_iBi​ is the name of the ii−th person coming to Alisha's party and B_iBi​ brings a gift of value v_ivi​.

Each of the following mm lines contains two integers t(1le t le k)t(1≤t≤k) and p(0 le p le k)p(0≤p≤k) separated by a blank. The door will open right after the tt−th person arrives, and Alisha will let pp friends enter her castle.

The last line of each test case will contain qq numbers n_1, ..., n_qn1​, ..., nq​ separated by a space, which means Alisha wants to know who are the n_1-th, ..., n_q-thn1​−th, ..., nq​−th friends to enter her castle.

Note: there will be at most two test cases containing n > 10000n>10000.

Output Format

For each test case, output the corresponding name of Alisha's query, separated by a space.

样例输入

1
5 2 3
Sorey 3
Rose 3
Maltran  3
Lailah 5
Mikleo  6
1 1
4 2
1 2 3

样例输出

Sorey Lailah Rose


模拟题

 

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 150010;
int n, m, t, x, k, q;
struct Nod{
    char s[201];
    int id, v;
    bool friend operator < (const Nod &a , const Nod &b) {
        return ((a.v == b.v && a.id > b.id) || (a.v < b.v));
    }
}e[N];
struct Node{
    int t, p;
    bool friend operator < (const Node &a, const Node &b) {
        return a.t < b.t;
    }
}b[N];
Nod str[50000];
int main() {
    cin >> t;
    priority_queue<Nod> que;
    while(t--) {
        while(que.size()) que.pop();
        cin >> k >> m >> q;
        for(int i = 1; i <= k; i ++) {
            cin >> e[i].s >> e[i].v;
            e[i].id = i;
        }
        for(int i = 0; i < m; i ++) {
            scanf("%d%d",&b[i].t,&b[i].p);
        }
        sort(b,b+m);
        int cnt = 1, cnt1 = 1;
        for(int i = 0; i < m; i ++) {
            while(cnt <= b[i].t) que.push(e[cnt++]);
            for(int j = 0; j < b[i].p; j ++) {
                if(que.empty()) break;
                str[cnt1++] = que.top(), que.pop();
            }
        }
        while(cnt <= k) que.push(e[cnt++]);
        while(que.size()) str[cnt1++] = que.top(), que.pop();
        for(int i = 1; i <= q; i ++) {
            scanf("%d", &x);
            printf("%s%c",str[x].s," 
"[i==q]);
        }
    }
    return 0;
}

B Ponds

Betty owns a lot of ponds, some of them are connected with other ponds by pipes, and there will not be more than one pipe between two ponds. Each pond has a value vv.

Now Betty wants to remove some ponds because she does not have enough money. But each time when she removes a pond, she can only remove the ponds which are connected with less than two ponds, or the pond will explode.

Note that Betty should keep removing ponds until no more ponds can be removed. After that, please help her calculate the sum of the value for each connected component consisting of a odd number of ponds

Input Format

The first line of input will contain a number T(1 le T le 30)T(1≤T≤30) which is the number of test cases.

For each test case, the first line contains two number separated by a blank. One is the number p(1 le p le 10^4)p(1≤p≤104)which represents the number of ponds she owns, and the other is the number m(1 le m le 10^5)m(1≤m≤105) which represents the number of pipes.

The next line contains pp numbers v_1, ..., v_pv1​, ..., vp​, where v_i(1 le v_i le 10^8)vi​(1≤vi​≤108) indicating the value of pond ii.

Each of the last mm lines contain two numbers aa and bb, which indicates that pond aa and pond bb are connected by a pipe.

Output Format

For each test case, output the sum of the value of all connected components consisting of odd number of ponds after removing all the ponds connected with less than two pipes.

样例输入

1
7 7
1 2 3 4 5 6 7
1 4
1 5
4 5
2 3
2 6
3 6
2 7

样例输出

21

dfs搜索下就行。

#include <bits/stdc++.h>
#define ll unsigned     long long
using namespace std;
const int N = 10010;
int n, m, t, u, v, p, cnt;
ll a[N];
std::vector<int> vs[N], vv;
int vis[N], vis1[N];

bool ok(int x) {
    int ans = 0;
    for(auto u : vs[x]) {
        if(!vis[u]) ans++;
    }
    return ans < 2;
}

void dfs(int v) {
    vis[v] = 1;
    for(auto u : vs[v]) {
        if(!vis[u]&&ok(u)) dfs(u);
    }
}
void dfs1(int v) {
    vis1[v] = 1;
    for(auto u : vs[v]) {
        if(!vis[u]&&!vis1[u]) {
            vv.push_back(u);
            dfs1(u);
        }
    }
}

int main() {
    cin >> t;
    while(t--) {
        memset(vis, 0, sizeof(vis));
        memset(vis1, 0, sizeof(vis1));
        cin >> p >> m;
        for(int i = 1; i <= p; i ++) scanf("%lld", &a[i]);
        for(int i = 0; i < m; i ++) {
            scanf("%d%d", &v, &u);
            vs[v].push_back(u);
            vs[u].push_back(v);
        }
        for(int i = 1; i <= p; i ++) {
            if(!vis[i]&&ok(i)) dfs(i);
        }
        // for(int i = 1; i <= p; i ++) printf("%d ",vis[i]);printf("
");
        for(int i = 1; i <= p; i ++) {
            if(!vis[i]&&!vis1[i]) {
                vv.clear();
                vv.push_back(i);
                dfs1(i);
                // printf("-=%d-=
", vv.size());
                if(vv.size()%2 == 0) {
                    for(int j = 0; j < vv.size(); j ++) vis1[vv[j]] = 2;
                }
            }
        }
        // for(int i = 1; i <= p; i ++) printf("%d ",vis1[i]);printf("
");
        ll ans = 0;
        for(int i = 1; i <= p; i ++) if(vis1[i]==1) ans += a[i];
        printf("%lld
",ans);
        for(int i = 1; i <= p; i ++) vs[i].clear();
    }
    return 0;
} 

E Travel

Jack likes to travel around the world, but he doesn’t like to wait. Now, he is traveling in the Undirected Kingdom. There are nn cities and mm bidirectional roads connecting the cities. Jack hates waiting too long on the bus, but he can rest at every city. Jack can only stand staying on the bus for a limited time and will go berserk after that. Assuming you know the time it takes to go from one city to another and that the time Jack can stand staying on a bus is xx minutes, how many pairs of city (a, b)(a, b) are there that Jack can travel from city aa to bbwithout going berserk?

Input Format

The first line contains one integer T, Tle 5T, T≤5, which represents the number of test case.

For each test case, the first line consists of three integers n, mn, m and qq where n le 20000, mle 100000, qle 5000n≤20000, m≤100000, q≤5000. The Undirected Kingdom has nn cities and mm bidirectional roads, and there are qq queries.

Each of the following mm lines consists of three integers a, ba, b and dd where a, bin {1, ..., n}a, b∈{1, ..., n} and d le 100000d≤100000. It takes Jack dd minutes to travel from city aa to city bb and vice versa.

Then qq lines follow. Each of them is a query consisting of an integer xx where xx is the time limit before Jack goes berserk.

Output Format

You should print qq lines for each test case.

Each of them contains one integer as the number of pair of cities (a, b)(a, b) which Jack may travel from aa to bb within the time limit xx.

Note that (a, b)(a, b) and (b, a)(b, a) are counted as different pairs and aa and bb must be different cities.

样例输入

1
5 5 3
2 3 6334
1 5 15724
3 5 5705
4 3 12382
1 3 21726
6000
10000
13000

样例输出

2
6
12

先预处理下，排下序，假设选取前面 i 个的答案是多少，计算出来。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e5+10;
int n, m, t, q, x, y, sum[N], fa[N], cnt[N];
set<int> st;
struct Nod{
    int from, to, w;
}e[N];
bool cmp(Nod a, Nod b) {
    return a.w < b.w;
}
int find(int x) {
    return fa[x] = (fa[x] == x ?x: find(fa[x]));
}
void unite(int x, int y) {
    x = find(x), y = find(y);
    if(x > y) fa[x] = y;
    else fa[y] = x;
}
int bin(int x) {
    int l = 1, r = m;
    while(l < r) {
        int mid = (l+r)>>1;
        if(e[mid].w <= x) l = mid+1;
        else r = mid;
    }
    return r-1;
}

int main() {
    cin >> t;
    while(t--) {
        scanf("%d%d%d", &n, &m, &q);
        st.clear();
        for(int i = 1; i <= n; i ++) fa[i] = i, cnt[i] = 1;
        for(int i = 1; i <= m; i ++) scanf("%d%d%d",&e[i].from,&e[i].to,&e[i].w);
        sort(e+1,e+1+m,cmp);
        for(int i = 1; i <= m; i ++) {
            x = find(e[i].from), y = find(e[i].to);
            if(x != y) {
                sum[i] = sum[i-1];
                if(st.count(x)) sum[i] -= cnt[x]*(cnt[x]-1);
                if(st.count(y)) sum[i] -= cnt[y]*(cnt[y]-1);
                sum[i] += (cnt[x]+cnt[y])*(cnt[x]+cnt[y]-1);
                st.insert(min(x,y));
                st.erase(max(x,y));
                cnt[min(x,y)] += cnt[max(x,y)];
                cnt[max(x,y)] = 0;
                unite(x,y);
            } else sum[i] = sum[i-1];
        }
        // for(int i = 1; i <= m; i ++) printf("%d ",sum[i]);printf("
");
        while(q--) {
            scanf("%d", &x);
            if(x >= e[m].w) printf("%d
",sum[m]);
            else printf("%d
",sum[bin(x)]);
        }
    }
    return 0;
}

G The Water Problem

In Land waterless, water is a very limited resource. People always fight for the biggest source of water.

Given a sequence of water sources with a_1, a_2, a_3, ..., a_na1​, a2​, a3​, ..., an​ representing the size of the water source.

Given a set of queries each containing 22 integers ll and rr, please find out the biggest water source between a_lal​and a_rar​.

Input Format

First you are given an integer T(Tle 10)T(T≤10) indicating the number of test cases.

For each test case, there is a number n(0 le n le 1000)n(0≤n≤1000) on a line representing the number of water sources.

nn integers follow, respectively a_1, a_2, a_3, ..., a_na1​, a2​, a3​, ..., an​, and each integer is in {1, ..., 10^6}{1, ..., 106}.

On the next line, there is a number q(0 le q le 1000)q(0≤q≤1000) representing the number of queries.

After that, there will be qq lines with two integers ll and r(1 le l le r le n)r(1≤l≤r≤n) indicating the range of which you should find out the biggest water source.

Output Format

For each query, output an integer representing the size of the biggest water source.

样例输入

3
1
100
1
1 1
5
1 2 3 4 5
5
1 2
1 3
2 4
3 4
3 5
3
1 999999 1
4
1 1
1 2
2 3
3 3

样例输出

100
2
3
4
4
5
1
999999
999999
1

板子题，求区间最大。

#include <iostream>
#include <cstdio>
#define lson l, m, rt<<1
#define rson m+1,r, rt<<1|1

using namespace std;
const int maxn = 1e5+2;
int MAX[maxn<<2];
int max(int a, int b){
    return a>b?a:b;
}
void PushDP(int rt){
    MAX[rt] = max(MAX[rt<<1], MAX[rt<<1|1]);
}
void build(int l, int r, int rt){
    if(l == r){
        scanf("%d",&MAX[rt]);
        return;
    }
    int m = (l + r) >> 1;
    build(lson);
    build(rson);
    PushDP(rt);
}
void update(int x, int y, int l, int r, int rt){
    if ( l == r){
        MAX[rt] = y;
        return ;
    }
    int m = (l + r) >> 1;
    if(x <= m) update(x, y, lson);
    else update(x, y, rson);
    PushDP(rt);
}
int Query(int L, int R, int l, int r, int rt){
    if(L <= l && R >= r){
        return MAX[rt];
    }
    int m = (l + r) >> 1;
    int ret = 0;
    if( m >= L) ret = max(ret, Query(L, R ,lson));
    if( m < R) ret = max(ret, Query(L, R, rson));
    return ret;
}
int main()
{
    int t, n, m, q, l, r;
    cin >> t;
    while(t--){
        cin >> n;
        build(1, n, 1);
        cin >> q;
        while(q--) {
            cin >> l >> r;
            printf("%d
",Query(l, r, 1, n, 1));
        }
    }
    return 0;
}

H Elven Postman

•  131072K

 

Elves are very peculiar creatures. As we all know, they can live for a very long time and their magical prowess are not something to be taken lightly. Also, they live on trees. However, there is something about them you may not know. Although delivering stuffs through magical teleportation is extremely convenient (much like emails). They still sometimes prefer other more “traditional” methods.

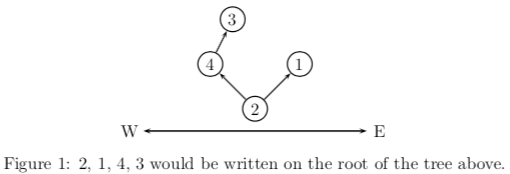
So, as a elven postman, it is crucial to understand how to deliver the mail to the correct room of the tree. The elven tree always branches into no more than two paths upon intersection, either in the east direction or the west. It coincidentally looks awfully like a binary tree we human computer scientist know. Not only that, when numbering the rooms, they always number the room number from the east-most position to the west. For rooms in the east are usually more preferable and more expensive due to they having the privilege to see the sunrise, which matters a lot in elven culture.

Anyways, the elves usually wrote down all the rooms in a sequence at the root of the tree so that the postman may know how to deliver the mail. The sequence is written as follows, it will go straight to visit the east-most room and write down every room it encountered along the way. After the first room is reached, it will then go to the next unvisited east-most room, writing down every unvisited room on the way as well until all rooms are visited.

Your task is to determine how to reach a certain room given the sequence written on the root.

For instance, the sequence 2, 1, 4, 32, 1, 4, 3 would be written on the root of the following tree.

Input Format

First you are given an integer T(Tle 10)T(T≤10) indicating the number of test cases.

For each test case, there is a number n(nle 1000)n(n≤1000) on a line representing the number of rooms in this tree. nnintegers representing the sequence written at the root follow, respectively a_1, ..., a_na1​, ..., an​ where a_1, ..., a_nin {1, ..., n}a1​, ..., an​∈{1, ..., n}.

On the next line, there is a number qq representing the number of mails to be sent.

After that, there will be qq integers x_1, ..., x_qx1​, ..., xq​ indicating the destination room number of each mail.

Output Format

For each query, output a sequence of move (EE or WW) the postman needs to make to deliver the mail. For that EEmeans that the postman should move up the eastern branch and WW the western one. If the destination is on the root, just output a blank line would suffice.

Note that for simplicity, we assume the postman always starts from the root regardless of the room he had just visited.

样例输入

2
4
2 1 4 3
3
1 2 3
6
6 5 4 3 2 1
1
1

样例输出

E

WE
EEEEE

二叉排序树的建立与查找，找过的点就不需要找了。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1010;
int t, n, q, x;
struct Nod{
    int num;
    bool is;
    Nod *lchild, *rchild;
    Nod() {
        num = -1;
        is = false;
        lchild = rchild = NULL;
    }
};
void mkTree(Nod *p, int val) {
    if(p->num == -1) {
        p->num = val;
        return;
    }
    if(p->num > val) {
        if(p->rchild==NULL)p->rchild = new Nod;
        mkTree(p->rchild,val);
    } else {
        if(p->lchild==NULL)p->lchild = new Nod;
        mkTree(p->lchild,val);
    }
}
void find(Nod *p, int x) {
    if(p->num == x) {
        if(!p->is) {
            p->is = true;
            return;
        }
    }
    if(p->num > x) {
        printf("E");
        find(p->rchild,x);
    } else {
        printf("W");
        find(p->lchild, x);
    }
}
int main() {
    cin >> t;
    while(t--) {
        scanf("%d", &n);
        Nod *root = new Nod;
        for(int i = 1; i <= n; i ++) {
            scanf("%d", &x);
            mkTree(root,x);
        }
        scanf("%d", &q);
        while(q--) {
            scanf("%d", &x);
            find(root,x);printf("
");
        }
    }
    return 0;
}

J Unknown Treasure

•  131072K

 

On the way to the next secret treasure hiding place, the mathematician discovered a cave unknown to the map. The mathematician entered the cave because it is there. Somewhere deep in the cave, she found a treasure chest with a combination lock and some numbers on it. After quite a research, the mathematician found out that the correct combination to the lock would be obtained by calculating how many ways are there to pick mm different apples among nn of them and modulo it with MM. MM is the product of several different primes.

Input Format

On the first line there is an integer T(Tle 20)T(T≤20) representing the number of test cases.

Each test case starts with three integers n, m, k(1le mle nle 10^{18}, 1le kle 10)n, m, k(1≤m≤n≤1018, 1≤k≤10) on a line where kk is the number of primes.

Following on the next line are kk different primes p_1, ..., p_kp1​, ..., pk​. It is guaranteed that M=p_1 imes p_2 imes cdots imes p_kle 10^{18}M=p1​×p2​×⋯×pk​≤1018 and p_ile 10^5pi​≤105 for every iin{1, ..., k}i∈{1, ..., k}.

Output Format

For each test case output the correct combination on a line.

样例输入

1
9 5 2
3 5

样例输出

6

求C(n,m)%M  M = p1*p2..*pk   Lucas定理。

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 15;
ll qmul(ll a,ll p,ll m){
    ll tmp = 0;
    while(p){
        if(1&p) tmp = (tmp+a)%m;
        a = (a+a)%m;
        p>>=1;
    }
    return tmp;
}
void exgcd(ll a,ll b,ll &x,ll &y,ll &d){
    if(!b) d=a,x = 1,y=0;
    else exgcd(b,a%b,y,x,d),y-=(a/b)*x;
}
ll inv(ll a,ll p){
    ll x,y,d;
    exgcd(a,p,x,y,d);
    return d==1?(x+p)%p:-1;
}
ll fat(ll x,ll p){
    ll ans = 1;
    for( int i = 2 ; i <= x ; i ++ ) ans = ( ans * i ) % p;
    return ans;
}
ll c(ll n,ll m,ll p){
    if (m < 0 || m > n) return 0; 
    return fat(n,p)*inv(fat(m,p),p)%p*inv(fat(n-m,p),p)%p;
}
ll crt(ll *a,ll *m,int n){
    ll M = 1,res = 0;
    for( int i = 0 ; i < n ; i++ ) M*=m[i];
    for( int i = 0 ; i < n ; i++ ){
        ll w = M/m[i];
        res = (res+qmul(w*inv(w,m[i]),a[i],M))%M;
    }
    return (res+M)%M;
}
ll Lucas(ll n,ll m,ll p){
    return m?Lucas(n/p,m/p,p)*c(n%p,m%p,p)%p:1;
}
int main() {
    ll a[N], p[N];
    ll t, n, m, k;
    cin >> t;
    while(t--) {
        cin >> n >> m >> k;
        for(int i = 0; i < k; i ++) {
            cin >> p[i];
            a[i] = Lucas(n, m, p[i]);
        }
        printf("%lld
",crt(a, p, k));
    }
    return 0;
}