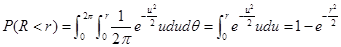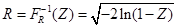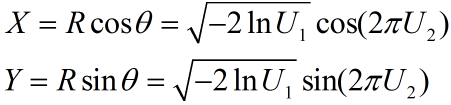作者：桂。
时间：2017-03-12 19:31:55
链接：http://www.cnblogs.com/xingshansi/p/6539319.html
前言
本文是曲线拟合与分布拟合一文的插曲，进行分布拟合时，碰到一个问题是，如何指定分布的随机数呢？本文主要包括：
1）连续型随机数；
2）离散型随机数；
本文内容为自己的学习笔记，内容多有借鉴他人，在最后一并给出链接。
一、连续型随机数
假设已经拥有U（0，1）的均匀分布数据。
A-逆变换法（Inverse Transform Method）
如果我们可以给出概率分布的累积分布函数（F）及其逆函数的解析表达式，则可以非常简单便捷的生成指定分布随机数。
性质：
U是服从[0，1]均匀分布的随机变量，如果$X = F^{-1}(U)$，则X的分布函数与F相同，即$F_X(x) = F$.
证明：
$F_X(a) = P(X le a) = P(F^{-1}(U) le a) = P(U le F(a)) = F(a)$.即$F_X$与F相同，得证。
算法步骤：
- 生成一个服从均匀分布的随机数U~Unit(0,1);
- 设F(x)为指定分布的分布函数，则$X = F^{-1}（U）$即为指定分布的随机数。
示例：生成满足$lambda = 2$的指数分布随机数。
分析：
由$f(x)$得出$F(x)$ —> $F(x) = 1 - {e^{ - lambda x}}$，进而求得$F(x)$逆函数，得出$X = {F^{ - 1}}(u) = - frac{1}{lambda }ln (1 - u)$.
代码：
Len = 1000000; u = rand(1,Len); lemda = 2; x = -1/lemda*(log(1-u));
对应结果：
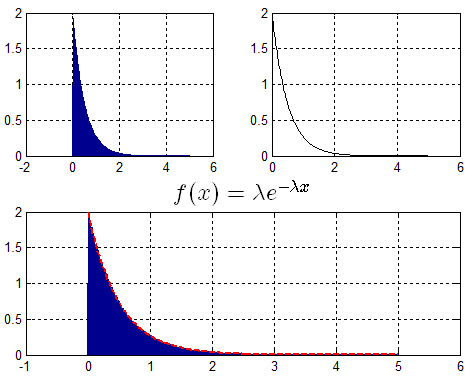
B-舍选法（Acceptance-Rejection Method）
一般来说逆变换法是一种很好的算法，简单且高效，如果可以使用的话，是第一选择。但是逆变换法有自身的局限性，就是要求必须能给出分布函数F逆函数的解析表达式，有些时候要做到这点比较困难，这限制了逆变换法的适用范围。
当无法给出分布函数F逆函数的解析表达式时，舍选法是另外的选择。舍选法的适用范围比逆变换法要大，只要给出概率密度函数的解析表达式即可，而大多数常用分布的概率密度函数是可以查到的。
算法思想：
给定轮廓，并在轮廓范围内生成均匀分布序列；
算法实现：
- 设概率密度函数为$f(x)$，首先生成一个均匀分布随机数X~Unit($x_{min}$，$x_{max}$);
- 独立地生成一个均匀分布随机数Y~Unit($y_{min}$，$y_{max}$);
- 若$Y le f(X)$，则返回X，否则重复第一步。
给出一张舍选法的原理图：
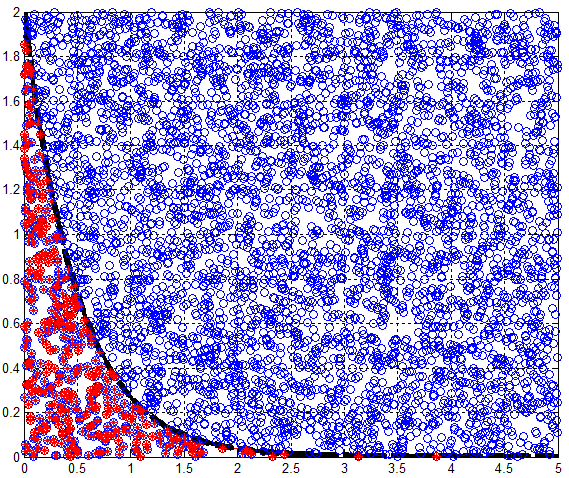
代码（data即为最终的随机数）：
xmin = 0; xmax = 5; Len = 1000000; x = (xmax-xmin)*rand(1,Len)-xmin; lemda = 2; fx = lemda*exp(-lemda*x); ymax = lemda; ymin = 0; Y = (ymax-ymin)*rand(1,Len)-ymin; data = x(Y<=fx);
结果图：
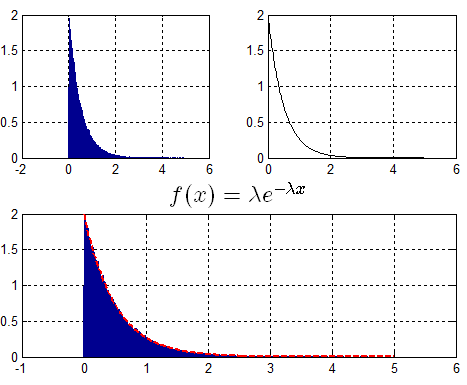
舍选法需要对数据重复筛选，性能不如逆变换法，但其适应性更广，无法得到分布函数的逆函数时，舍选法不失为一个选择。
其实本质就是取分布以内的随机数，颠倒过来，给定分布，将分布无限细分，生成各区间对应数量的随机数，也可以实现近似。
C-组合法
当目标分布可以用其它分布经过四则运算表示时，可以使用组合算法生成对应随机数。此部分仅以几个例子简要介绍。
例一：正态分布（Box Muller方法）
正态分布随机数的产生，除了上文的方式，经典的就是Box Muller方法，所有正态分布均可由标准正态分布演变得出。
Box Muller理论推导：
设$(X,Y)$是一对相互独立的服从正态分布$N(0,1)$的随机变量，则有概率密度函数（指数少一负号）：
转化为极坐标形式，令
，则R有分布：
Eq.(1)
令
，则分布函数的反函数为：
由逆变换法性质可知：
满足$F_R$的分布可由$1-Z$~$U(0,1)$得出，亦即：可由$Z$~$U(0,1)$得出；
再分析$P_{ heta}$，同样对Eq.(1)中表达式关于$r$进行从0到∞的积分，容易得出$ heta$服从均匀分布，因此该随机数可由均匀分布直接产生；
又易证$P(r; heta)=P(r)P( heta)$，即二者独立，因此二者可由不同的均匀分布分别生成。
以上为Box Muller的原理分析。
Box Muller算法实现：
- 分别生成两组均匀分布随机数：$U_1$~$U(0,1)$、$U_2$~$U(0,1)$；
- 生成$R$以及$ heta$的分布：
- 生成两组独立的标准正态分布:
- 生成符合给定均值、方差具体要求的正态分布；
代码(生成标准正态分布)：
Len = 10000; U1 = rand(1,Len); U2 = rand(1,Len); R = sqrt(-2*log(U1)); theta = 2*pi*U2; X = R.*cos(theta); Y = R.*sin(theta);
效果图：
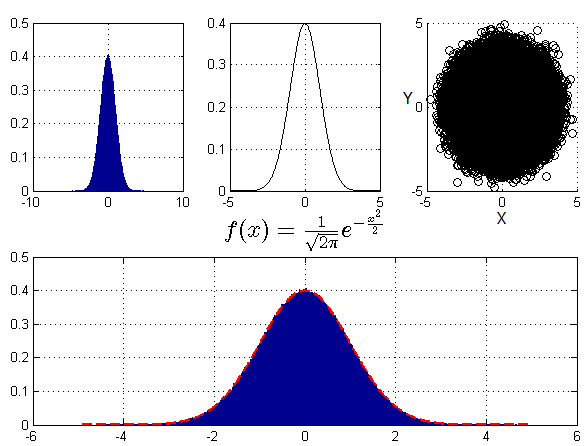
啰嗦一句：从scatter(X,Y)的结果中，可以直观看出X、Y不相关，但不能确定不独立。$X*Y = (X,Y)$与$P_X*P_Y =P (X,Y)$不是一个概念。对于同样一个圆形区域，X、Y可以按不同的密度分布落入。
再看看均匀分布的scatter(X,Y)：
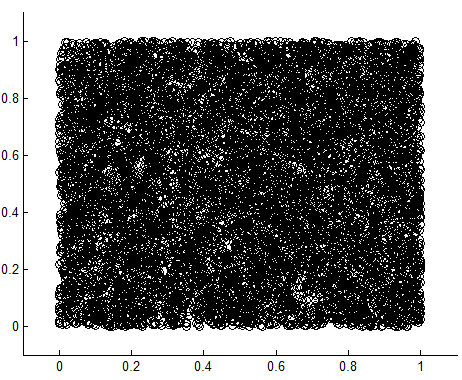scatter结果：一个圆形、一个方形，但两种情况下X、Y都是独立同分布的。
例二：瑞利分布（Rayleigh Distribution）
其实Box Muller方法的中间过程，包含了瑞利分布，即$P(r)$。给出PDF定义式：
$f(r) = frac{r}{{{sigma ^2}}}{e^{ - frac{{{r^2}}}{{2{sigma ^2}}}}}$
其中$sigma > 0$.
理论分析：
设$(X,Y)$是一对相互独立的服从正态分布$N(0,sigma ^2)$的随机变量，则有概率密度函数：
$fleft( {x,y} ight) = f(x)f(y) = frac{1}{{2pi {sigma ^2}}}{e^{ - frac{{{x^2} + {y^2}}}{{2{sigma ^2}}}}}$
转化为极坐标，$dxdy = rdrd heta $，并对$ heta$求取积分，得：
$fleft( r ight) = frac{r}{{{sigma^2}}}{e^{ - frac{{{r^2}}}{{2{sigma ^2}}}}}$
可见：设$(X,Y)$是一对相互独立的服从正态分布$N(0,sigma ^2)$的随机变量，按Box Muller的方法构造R，即为对应的瑞利分布。
回顾公式：$R = sqrt {{X^2} + {Y^2}} $，两个独立同正态分布（零均值）信号的包络是瑞利分布。
算法步骤：
- 生成一组均匀分布随机数：$U$~$U(0,1)$；
- 根据给定的参数$sigma$，生成：$R = sigma sqrt { - 2ln U} $;R即为满足要求的瑞利分布；
对应代码：
Len = 1000000; U1 = rand(1,Len); U2 = rand(1,Len); sigma = 2; R = sigma*sqrt(-2*log(U1));
结果图：
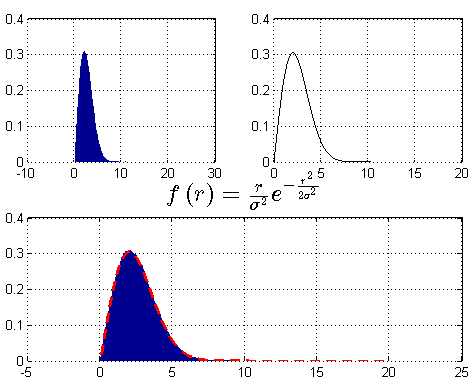
例三：泊松分布（Poisson distribution）
- 背景介绍
一段时间内，事件发生的次数，组成计数过程。泊松分布是一种常用的计数过程。
生活中，大量事件是有固定频率的，即可以通过一段时间内计数找出规律：
- 某医院平均每小时出生3个婴儿
- 某公司平均每10分钟接到1个电话
- 某超市平均每天销售4包xx牌奶粉
- 某网站平均每分钟有2次访问
这里不展开讲泊松分布的来龙去脉，直接给出公式：
再来回顾指数分布，指数分布描述的是：计数过程中，相邻事件发生的时间间隔概率分布。
对应上面的问题，则有
- 婴儿出生的时间间隔
- 来电的时间间隔
- 奶粉销售的时间间隔
- 网站访问的时间间隔
指数分布可由泊松分布推出：
泊松分布 —> 指数分布：
设相邻两次事件间隔为$T$，起始时刻为$T_{start}$，则终止时刻为$T_{start}+T$，$P{ T ge t }$表示$[T_{start},T_{start}+t]$时间内没有事件发生，即：
从而事件发生的概率为：
对应概率密度为：
对于泊松分布，得出结论：
- 两次事件的时间间隔为负指数分布，且均值为$frac{1}{lambda }$;
- 事件1与事件2，事件2与事件3，...事件n与事件n+1，相邻事件的时间间隔具有独立同分布的特性。
- 算法实现
此处给出的泊松分布随机数，产生原理基于指数分布，更多方法可以戳这里。
首先给出算法思想与算法步骤：
算法思想：
根据上文分析可知，Poisson分布对应一段时间内（记为$t_{max}$）事件发生次数，而指数分布exp对应相邻时间的时间分布;
反过来，已知两两相邻的时间变量，该变量服从指数分布且相互独立，所有时间变量相加—>并让其不超过一段时间的总量$t_{max}$，则累加数的分布对应泊松（Poisson）分布。
算法步骤：
- 生成一组均匀分布随机数：$U$~$U(0,1)$;
- 利用逆变换法生成一系列独立的指数分布$X_i$ ~ $exp(lambda )$;
- 记
如果$Y > t_{max}$，则停止，并输出$k-1$;否则，继续生成$X_{k+1}$，直到$Y > t_{max}$为止；
- 循环操作过程3；
输出的一系列整数（值为$k-1$）服从参数为$mu = lambda t_{max}$的Poisson分布。
由于上文已经交代如何生成指数分布，代码中直接调用指数随机量exprnd函数，不再重复生成；本文主要讲究思路，事实上，本文列举的例子都有现成的函数调用。
给出代码（data即为生成的数据）：
Iter = 10000; % 迭代次数，即data个数
lambda = 2;
t_max = 11;
%phei = lambda*t_max;%均值
for m=1:Iter,
k=1;
Y(m,1)=exprnd(1/lambda);
while Y(m,k) <= t_max % 时间间隔 (0,t_max]
Y(m,k+1)=Y(m,k)+exprnd(1/lambda);
k=k+1;
end
data(m)=k-1;
end
测试结果(将代码生成结果与MATLAB自带函数poissrnd.m的结果对比)：
二、离散型随机数
假设已经拥有U（0，1）的均匀分布数据，离散型随机数根据[0,1]划分区间，给出对应变量值即可。
例：离散随机变量X的分布率如下表，试生成该随机数。
| X | -1 | 1 | 3 |
| P（x） | 0.7 | 0.2 | 0.1 |
tag = rand(1,1000); data = tag; data(tag>0.9) = 3; data(tag<=0.7) = -1; data(abs(data)<1) = 1;
直方图结果：
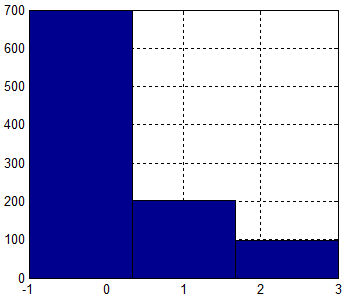
可以看出结果服从指定的分布率。
补充：本文仅简要介绍一维分布随机数的生成方式，有两个主要的点没有涉及：
- 均匀分布随机数的产生方式；
- 多维随机数的产生方式。
参考：