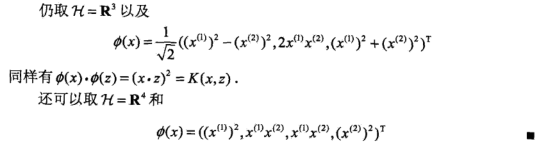作者：桂。
时间：2017-04-26 12:17:42
链接：http://www.cnblogs.com/xingshansi/p/6767980.html
前言
之前分析的感知机、主成分分析（Principle component analysis, PCA）包括后面看的支撑向量机（Support vector machines, SVM），都有用到核函数。核函数是将信号映射到高维，而PCA一般用来降维。这里简单梳理一下核函数的知识：
1）核函数基本概念;
2）核函数的意义;
内容为自己的学习记录，其中多有参考他人，最后一并给出链接。
一、核函数基本概念
先来看看核函数的定义：
核函数：是映射关系
的内积，映射函数本身仅仅是一种映射关系，并没有增加维度的特性，不过可以利用核函数的特性，构造可以增加维度的核函数，这通常是我们希望的。
例如这样一个图：
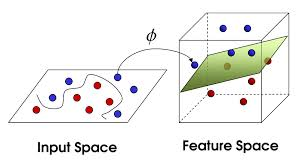
二维映射到三维，区分就更容易了，这是聚类、分类常用核函数的原因。为什么PCA这样一个降维算法也用核函数呢？
左图为原数据，右图为映射到三维的数据，可以看出：同样是降到1维，先通过Kernel映射到（Kernel是映射的内积，不要弄乱了）三维，再投影到1维，就容易分离开，这就是Kernel在PCA降维中的应用，本质还是对原有数据增加维度。
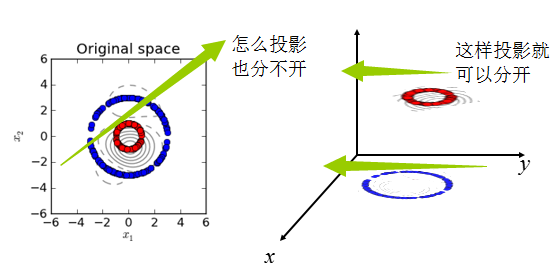
既然核函数这么神奇，就看看它的来龙去脉。
二、核函数的意义
A-核函数常见应用
先来看看核函数几个常用的地方：
1.核感知机
在前面分析感知机时提到：
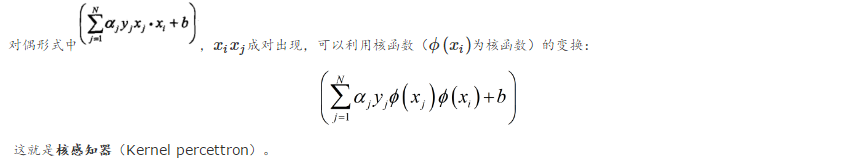
2.核聚类（Kernel Kmeans）
在前面分析核聚类时提到：
3.核PCA（kernel PCA）
具体定义可以参考wikipedia，根据前文分析的PCA步骤，有一步是利用相关矩阵的特征值分解，看看相关矩阵：
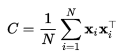
又看到了相乘的形式，自然可以用Kernel：
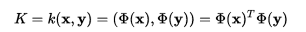
4.支撑向量机SVM
支撑向量机对偶形式的目标函数：
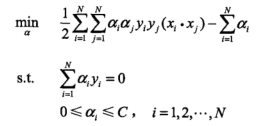
又看到了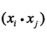
的形式，从而得到SVM的核函数形式：
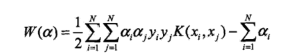
B-核函数为什么可以映射到高维？
1.为什么不用映射函数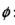
，而用他们的内积形式，即Kernel函数？
因为（x,z）一起出现的时候，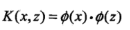
有许多固定的形式可以调用，而不必求解或者关心
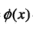的具体形式，这大大简化了求解。
2.什么样的函数才可以叫做核函数？
直接给出条件：
具体参考：李航《统计学习方法》p120~122。
3.为什么实现数据映射到高维？
看一个例子：
这就从二维变成了三维，当然还可以更高维：
这里可以粗略理解成：多项式可以实现数据的维度扩增，而高斯核是指数形式，展开就是无穷多的多项式，所以高斯核可以将数据映射到无穷维度。
4.常用核函数
多项式核：
高斯核：
参考：
- 李航《统计学习方法》