空间谱专题10：MUSIC算法

作者：桂。

时间：2017-09-19  19:41:40

链接：http://www.cnblogs.com/xingshansi/p/7553746.html 

---

前言

MUSIC（Multiple Signal Classification）算法通常用来进行到达角（DOA，Direction of arrival）估计。

一、MUSIC原理简介

根据前文的分析，模型依然建立在窄带信号的基础上：

X为接收阵元，F为入射信号，a为对应的导向矢量，W为噪声。可直接记作矩阵形式

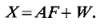
通常借助相关矩阵求解：

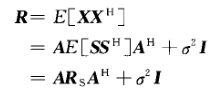
实际上相关矩阵无法得出，一般基于随机信号1）平稳性；2）遍历性 假设，近似估计相关矩阵：

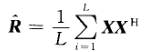
对相关矩阵进行特征值/奇异值分解，

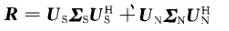
假设1）噪声与信号不相关；2）噪声为白噪声。 借助得到的特征向量，即可利用MUSIC算法求解角度： 

具体原理可以参考子空间算法一文。

二、相干情况分析

以两个信号为例

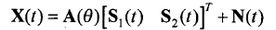
求相关矩阵

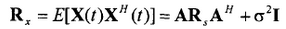
如果两个信号的相关系数ρ满足：

1）ρ=0，则认为两信号不相关；

2）0<ρ<1，则认为两信号相关；

3）ρ = 1，则两信号相干。

当两信号相干时，ρ=1，对于相关矩阵：

秩为1，这就造成了秩亏，对于子空间等空间谱估计算法便不再适用。

也可以换个角度理解：

两信号相干时，有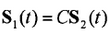，此时

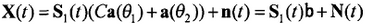
b称为广义阵列流行或广义导向矢量。可以看出它通常并不对应两个来波方向，而是二者的矢量叠加方向。一般的思路是希望将秩亏缺加以恢复。

三、特征值与峰值的关系

一种观点是，相关矩阵可分解为：

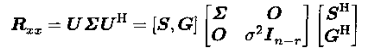
且对于导向矢量有：

那么对于导向矢量a(theta)：

a^HS∑S^Ha

不应该受∑特征值的影响而改变？为什么多个信号的时候，不同的theta对应的a(theta)，可以令峰值近似相等？或者说，为什么是对应真实角度时能量最大/最小？

a^HS∑S^Ha可进一步拆解为：

a^HS∑S^Ha = a^HA[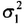,0;0,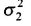^]A^Ha+M

M为阵元个数，对于任意方向均为常数，可忽略不计。 以两个信号为例，简化后的表达式为：

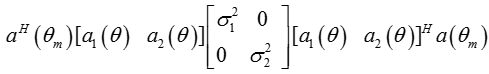
仿真验证：信号分别来自[-45°，45°]，功率近似相等：

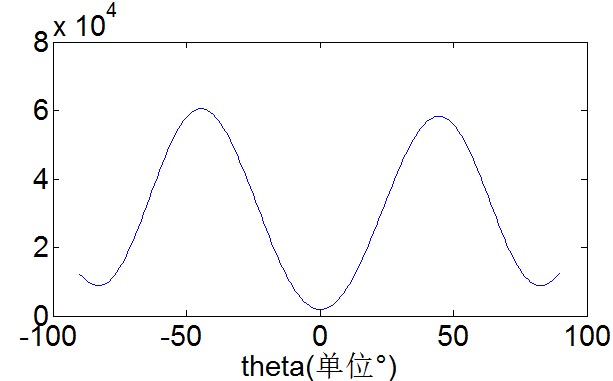
幅度近似为2倍关系：

 对于一维测向，假设坐标：

并认为一维线阵摆放在y轴上，对应的偏差为（打印为真实值，theta为理论值）

%目标坐标
dis = 400e3;%相距400km
theta = 50/180*pi ;%theta-[-50  50]
phi = 10/180*pi;
pos_tar = [dis*tan(phi), dis*sin(theta), dis*cos(theta)];
%阵元坐标
pos =[0 0 0;
      0 0.1 0];%相隔10cm
AB = [0 0.1 0];
AC = pos_tar;
BC = pos_tar-pos(2,:);
90-acos((sum(AB.^2)+sum(AC.^2)-sum(BC.^2))/2/sqrt(sum(AB.^2))/sqrt(sum(AC.^2)))/pi*180