作者:桂。
时间:2017-10-10 22:38:46
链接:http://www.cnblogs.com/xingshansi/p/7648274.html
前言
阵列信号处理中,经常用到小数延迟(fractional delay,FD)的思路,例如Beamforming、GSC等等,本文摘录几个小数延迟的实现方式,不打算做系统性的梳理,具体可参考课件。
一、问题模型
给出用到的资料:
1)部分code:网盘code.
2)stanford课件,对应链接:https://ccrma.stanford.edu/~jos/Interpolation/
3)Beamforming应用实例:http://www.labbookpages.co.uk/audio/beamforming/fractionalDelay.html
以均匀线阵为例:
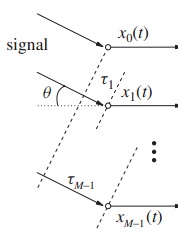
设麦克风阵列共用M个阵元,中心为参考点,阵元间距为d,信号入射角为θ,声音传播速度为c,则根据几何知识,第m(0≤m≤M-1)个阵元的时延为τm = (d/c) sinθ(m-(K-1)/2)。
麦克风采集的是数字信号,设采样周期为T,则对时域离散的信号来说,时延为D = τ/T。通常D不是一个整数,而对离散信号来说,整数时延才有意义。对于非整数D,可以分解为整数部分和分数部分D = ⌊D⌋ + d,式中,⌊D⌋为D的向下取整,0≤d<1。对于非零的分数部分d,此时信号实际值介于两个相邻采样点之间,即分数延迟。在实际处理中,可对d四舍五入取整,然后加上⌊D⌋,得到近似整数时延,但这种方法处理的结果不够精确。为了得到精确的结果,通常借助小数延迟的思路。
二、小数延迟滤波器
A-一阶FIR设计
思路主要来自Taloy一阶近似:

从而
![]()
即:
![]()
其中η为对应的小数延迟,滤波器架构(低通信号有效):

B-一阶IIR设计
此时对应的滤波器为全通滤波器(All pass),近似逼近
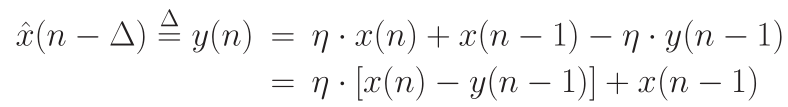
滤波器响应:
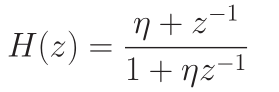
滤波器架构:

对应时间延迟:

C-Sinc逼近
根据小数延迟滤波器的特性:
- 幅度响应:全通
- 相位响应:线性
得出滤波器:

对于采样信号,需要限定在-fs/2 ~ fs/2之间,即相当于对滤波器进行了频域截断,截断的滤波器特性:
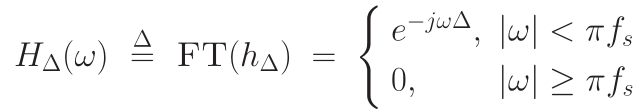
求解该滤波器:

容易证明该滤波器是原型滤波器均方误差最小的逼近。
%线阵为例 delay = d*sin(theta)*fs/c*(0:1:element_num); n = -64:63; i = 3;%延迟的阵元 h = sinc(n+delay(i)); H = zeros(1,256); H(1:128) = h; output = ifft((fft(sig)).*(fft(H)));%sig为输入信号 %相比时域卷积,频域点乘进一步节省资源
存疑:如果不是[-pi pi],而是取[0 2*pi],即sin(2*pi*f0*t)其中f0为大于fs/2的信号,简单的逼近结果错误,延迟如何实现?
已解决,具体参考:过采样的小数延迟实现。
D-Sinc加窗
由于C中滤波器存在截断,防止能量泄露的一个常用思路就是:加窗截断。
即:
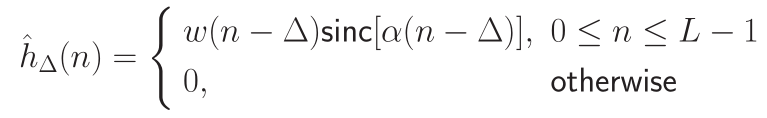
α < 1 provides for a nonzero transition band。
对应code:
function h = hsincw2(L,d,wp,win)
% HSINCW2
% MATLAB m-file for sinc windowing method for FD filter design
% h = hsincw2(L,d,wp,win) designs an (L-1)th-order FIR
% filter to approximate a fractional delay of d samples,
% where 0 <= d < 1, wp is the passband of approximation and
% win is a length-L window function
% (e.g., win = chebwin(L,ripple), with sidelope ripple in dB).
% Output: length-L filter coefficient vector h
% Function Calls: standard MATLAB functions and sinc.m
%
% Timo Laakso 23.12.1992
% Revised by Vesa Valimaki 19.10.1995
% Last modified 14.01.1996
N = L-1; % filter order
M = N/2; % middle value
if (M-round(M))==0 % if L is even...
D = M + d; % D = M + d
else D = M + d -0.5; % ...otherwise
end;
b = (0:N)-D; % sample instants
h = sinc(wp*b); % shifted & sampled sinc function
h = h.*win; % windowing by the given window function
E-拉格朗日插值
该思路主要是借助拉格朗日插值,近似得出小数延迟位置的数值。关于拉格朗日插值法的介绍有很多。
滤波器逼近:
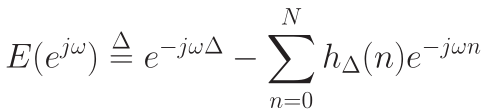
基于Taloy展开的性质:

这一特性符合拉格朗日插值的思路,利用此思路:

得出滤波器实现架构

对应code:
function h = lagrange(N, delay) %LAGRANGE h=lagrange(N,delay) returns order N FIR % filter h which implements given delay % (in samples). For best results, % delay should be near N/2 +/- 1. n = 0:N; h = ones(1,N+1); for k = 0:N index = find(n ~= k); h(index) = h(index) * (delay-k)./ (n(index)-k); end
不同插值个数对应的系数:
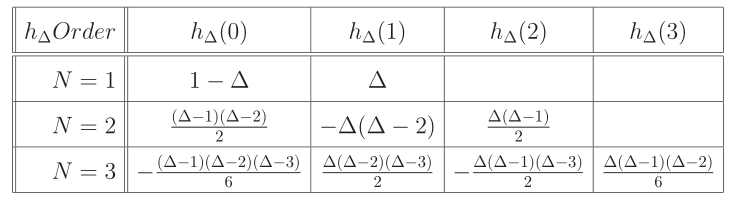
F-Farrow滤波器
该思路为多项式拟合,即将每一阶h看作是多项式拟合:

滤波器可表述为:
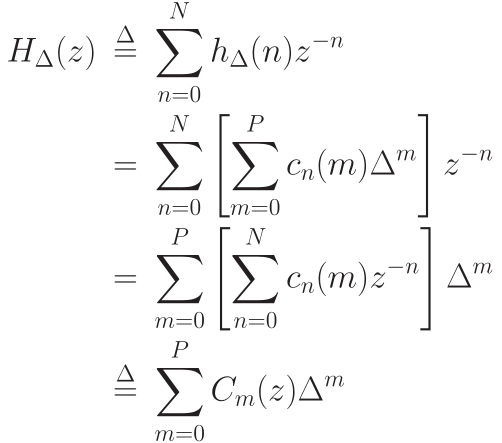
简化:
![]()
α可存在RAM里,利用查找表直接调用,便可以实现快速的小数延迟。
其中,参数求解:

对应实现架构:
