最近在刷吴恩达的coursea的机器学习视频,学完基于梯度下降的逻辑回归和基于梯度下降的神经网络后,就在反思这两者之间的区别,为什么必须使用神经网络?
逻辑回归不能替代神经网络么?他们的区别是什么呢?
答案:逻辑回归不能替代神经网络。
机器学习的本质其实是训练出一组参数,尽可能让基于这组参数的模型能正确识别出所有的样本。
然而,逻辑回归所有参数的更新是基于相同的式子,也就是所有参数的更新是基于相同的规则。 相比之下,神经网络每两个神经元之间参数的更新都基于不同式子,也就是每个参数的更新都是用不同的规则。
显而易见,神经网络模型能模拟和挖掘出更多复杂的关系,也具有更好的预测效果。下面详细分析逻辑回归的更新和神经网络的反向传播。
分析:逻辑回归的参数更新。 假设有m 个样本,他们的cost function(成本函数)为:
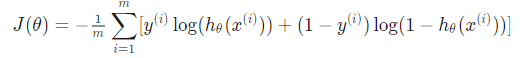 其中 h 函数为激活函数, xi为第 i 个样本, theta 为要训练的参数, 用向量的形式来写就是:
其中 h 函数为激活函数, xi为第 i 个样本, theta 为要训练的参数, 用向量的形式来写就是:
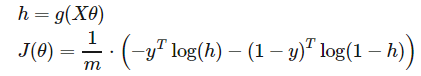
,其中X为代表所有样本的向量,是二维矩阵,每一行表示一个样本, Y为每一个样本本身应该属于的类。
对上面的cost function的每一个参数theta求偏导, 得到逻辑回归的所有参数的更新都根据的规则是: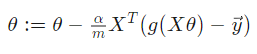 。
。
通过此式, 可以看出影响参数的更新的因素有 学习率a, 样本个数 m,样本输入X,样本所属于的类。
神经网络的参数更新过程: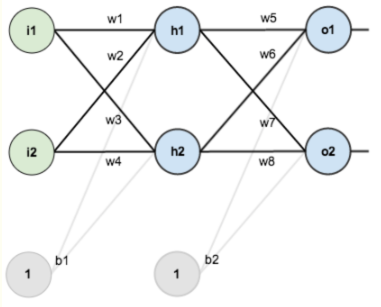
本文以上图神经网络为例,输入层有两个神经元,这两个神经元表示一个样本。 一个隐藏层, 两个输出。
正向传播: i1 ---h1 之间的传播,h1的输入为: ![]() 。
。
h1 的输出为: 假设用激活函数sigmoid, ![]() 。
。
h1---o1 之间的传播,o1的输入为:![]() 。
。
o1 的输出为: ![]()
反向传播:
(1)总误差(square error):
![]()
因为有2个输出, 所以error由两部分组成
![]()
![]()
(2)输出层与隐藏层间的参数更新:
以权重w5为例,![]()
计算![]() :
:
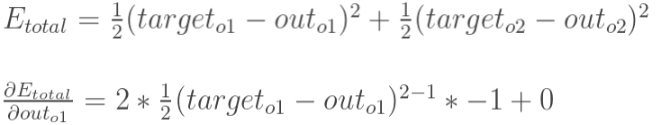
计算![]() :
:
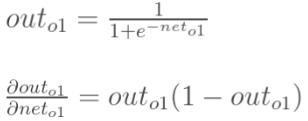
计算![]() :.
:.
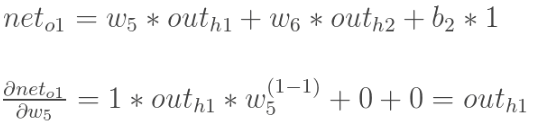
三者相乘,得到 w5 的更新为:
![]() (
(
w5的更新值主要与Out o1 和 Outh1相关)
同理,w6的更新取决于 Out o1 和 Outh2, W7 的更新取决于 Out o2 和 Outh1, W8 的更新取决于 Out o2 和 Outh2, 由此可见每个参数的更新式子都不同
(3)隐藏层与隐藏层间的参数更新:
计算W5时, 误差是从outo1 --neto1--w5 这样传递过来的。
而更新 w1 时, 路径是 outh1 ---neth1---w1, 而 outh1先要接收 Eo1 和 E 02 传来的误差。

![]() , 其中
, 其中 ![]()
通过计算可以得到,
![]()
所以, W1 的更新取决于Out o1 ,Out o2 , net01, net02, outh1, neth1.
即 W1的更新路径是(Out o1 ----- neto1 & Out o2 ----- neto2 )----- outh1 ----neth1 ----W1
W2 的更新路径是(Out o1 ----- neto1 & Out o2 ----- neto2 )----- outh1 ----neth1----W2
W3 的更新路径是(Out o1 ----- neto1 & Out o2 ----- neto2 )----- outh2 ----neth2----W3
由此可见, 神经网络的反向传播每个参数的路径是不一样的。