如下C#代码:
float a = 0.65f;
float b = 0.6f;
float c = a - b;
此时c为多少?
0.05?错误!
此时c为0.0499999523!
为什么?
其根本原因是计算机所使用二进制01代码无法准确表示某些带小数位的十进制数据。
下面我们来分析下:
我们知道将一个十进制数值转换为二进制数值,需要通过下面的计算方法:
1. 整数部分:连续用该整数除以2,取余数,然后商再除以2,直到商等于0为止。然后把得到的各个余数按相反的顺序排列。简称"除2取余法"。
2. 小数部分:十进制小数转换为二进制小数,采用"乘2取整,顺序排列"法。用2乘以十进制小数,将得到的整数部分取出,再用2乘余下的小数部分,然后再将积的整数部分取出,如此进行,直到积中的小数部分为0或者达到所要求的精度为止。然后把取出的整数部分按顺序排列起来,即先取出的整数部分作为二进制小数的高位,后取出的整数部分作为低位有效位。简称"乘2取整法"。
3. 含有小数的十进制数转换成二进制,整数、小数部分分别进行转换,然后相加。
例如:将十进制数值25.75转换为二进制数值,步骤如下:
25(整数部分)
25/2=12......1
12/2=6.......0
6/2=3......0
3/2=1......1
1/2=0......1
(25) 10=(11001) 2
0.75(小数部分)
0.75*2=1.5......1
0.5*2=1......1
(0.75) 10=(0.11) 2
(25.75) 10=(11001) 2+(0.11) 2=(11001.11) 2
按照上述方法,我们将0.65及0.6转换为二进制代码:
(0.65)10 = (0.101001100110011001100110011001100110011......)2
(0.6) 10 = (0.10011001100110011001100110011001100110011......)2
后面的省略号表示已经算不完了,后面在无限重复 0011 这段二进制数值。
文章开始部分,我们用的float类型,下面我们来看看float类型是否能存储上面转换出的二进制代码。
目前计算机上存储浮点数值是按照IEEE(电气和电子工程师协会)754浮点存储格式标准来存储的。
IEEE单精度浮点格式共32位,包含三个构成字段:23位小数f,8位偏置指数e,1位符号s。将这些字段连续存放在一个32位字里,并对其进行编码。其中0:22位包含23位的小数f; 23:30位包含8位指数e;第31位包含符号s。如下图所示: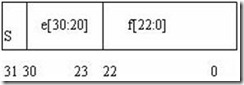
也就是说上面将0.65及0.5转换出的二进制代码,我们只能存储23位,即使数据类型为double,也只能存储52位,这样大家便能看出问题出现的原因了。
截取的二进制代码已无法正确表示0.65及0.5,根据这个二进制代码肯定无法正确得到结果0.05。
如何解决这个问题?知道其根本原因后,我们知道是无法从根本上解决这个问题的,但我们可以有一些曲线救国的方法,下面列举几个:
1. 因为二进制数值可以准确表示整数(可以使用整数转换为二进制方法验证下),所以可以将小数乘以10或100等变成整数,然后做运算,最后再通过除以10或100等获得结果;
2. 通过截取结果的有效小数位数等,来取得最好的近似结果,然后在做处理。
3. 对于可以用有限长度的二进制数值表示的十进制数值,可以使用存储位数大于其长度的数据类型。
解决方案正在补充中……,若各位有什么好的方法也可以提出来!
以上解决方案需要按照使用的实际情况来决定使用哪种方法。