Ex 6_21 最小点覆盖问题_第八次作业

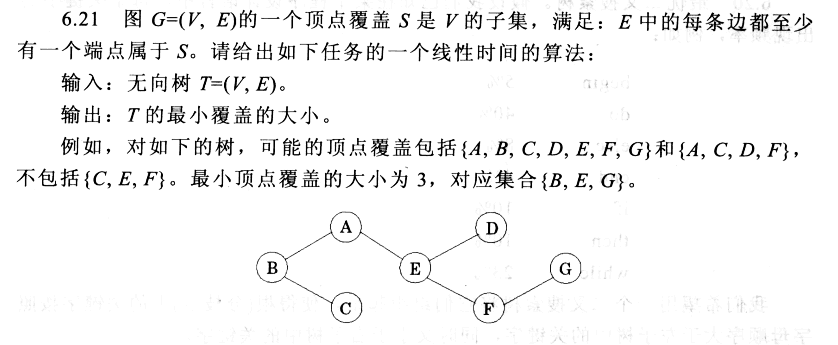
子问题定义: 对于图中的每个结点，有两种状态，即属于最小点覆盖和不属于最小点覆盖，定义minSet[i][0]表示结点i属于点覆盖，并且以i为根的树的最小点覆盖的大小。minSet[i][1]表示点i不属于点覆盖，并且以i为根的树的最小点覆盖的大小。

递归关系:

       对于minSet[i][0],i的孩子结点可以属于点覆盖，也可以不属于点覆盖，取其使以i为根的子树的点覆盖最小的情况，因此

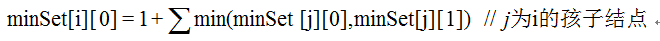
　　对于minSet[i][1],由于i不属于点覆盖，因此其所有孩子结点都必须属于点覆盖，因此

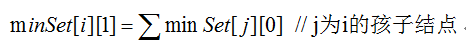
初值设定：

       minSet[i][0]=1

       minSet[i][1]=0

求解顺序：

       从树的叶子结点开始求每个结点的最小点覆盖，自底向上，最后比较minSet[root][0]与minSet[root][1]的大小，最小者即为最终的结果。

package org.xiu68.ch6.ex8;

import java.util.ArrayList;

public class Exp6_21 {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        //运行结果
        /*
         树的最大独立集为: 4
        顶点值为: 4 6 2 3 
        树的最小点覆盖为: 2
        顶点值为: 5 1 
        */
        //由结果可知 最大独立集与最小点覆盖集合互为补集
        ArrayList<Integer> vexs=new ArrayList<>();
        for(int i=1;i<=6;i++)
            vexs.add(i);
        //构造一个无向无环图
        int[][] edges=new int[][]{
            {0,1,1,0,0,0},
            {1,0,0,0,1,0},
            {1,0,0,0,0,0},
            {0,0,0,0,1,0},
            {0,1,0,1,0,1},
            {0,0,0,0,1,0}
        };
        MGraph<Integer> m=new MGraph<Integer>(6, 6, edges, vexs);
        m.maxIndependentSet();
        System.out.println();
        m.minCoverSet();
    }
}


//邻接矩阵表示图、无向无环图
class MGraph<T>{
    public int vexNum;                //顶点数量
    public int edgeNum;                //边数量
    public int[][] edges;            //邻接矩阵
    public ArrayList<T> vexs;        //顶点表
    
    public int[][] maxDep;                //最大独立集
    public ArrayList<Integer> set;        //最大独立集顶点序号
    
    public int[][] minCover;            //最小点覆盖
    public ArrayList<Integer> minSet;    //最小点覆盖顶点序号
    
    public MGraph(int vexNum, int edgeNum, int[][] edges, ArrayList<T> vexs) {
        this.vexNum = vexNum;
        this.edgeNum = edgeNum;
        this.edges = edges;
        this.vexs = vexs;
        
        maxDep=new int[vexNum][2];
        set=new ArrayList<>();
        
        minCover=new int[vexNum][2];
        minSet=new ArrayList<>();
    }
    
    //最大独立集
    public void maxIndependentSet(){
        independentSet(0, 0);

        if(maxDep[0][0]>maxDep[0][1])
            System.out.println("树的最大独立集为: "+maxDep[0][0]);
        else
            System.out.println("树的最大独立集为: "+maxDep[0][1]);
        
        System.out.print("顶点值为: ");
        for(int i=0;i<set.size();i++)
            System.out.print(vexs.get(set.get(i))+" ");
    }
    //求以child为根的树的最大独立集
    //child:当前正在处理的结点
    //parent:child的父结点
    private void independentSet(int child,int parent){
        maxDep[child][0]=1;        //当前结点放入独立集
        maxDep[child][1]=0;        //当前结点不放入独立集
    
        for(int i=0;i<vexNum;i++){
            if(edges[child][i]==0 || i==parent)    //如果顶点间不存在边或尾结点为父结点
                continue;
            independentSet(i, child);    
            
            //因为child加入了最大独立集，所以子结点不加入最大独立集
            //以child为根的树的最大独立集的规模为    ( 1+  child的孙子结点的最大独立集的规模  )
            maxDep[child][0]+=maxDep[i][1];       
            
            if(maxDep[i][0]>maxDep[i][1])
                maxDep[child][1]+=maxDep[i][0];        //加入子结点
            else
                maxDep[child][1]+=maxDep[i][1];        //不加入子结点
        }
        
        if(maxDep[child][0]>maxDep[child][1])    //比较加入child与不加入child的独立集大小，取较大者为结果
            set.add(child);
    }
    
    //***********************************************************

    //最小点覆盖
    public void minCoverSet(){
        coverSet(0,0);
        if(minCover[0][0]<minCover[0][1])
            System.out.println("树的最小点覆盖为: "+minCover[0][0]);
        else
            System.out.println("树的最小点覆盖为: "+minCover[0][1]);
        
        System.out.print("顶点值为: ");
        for(int i=0;i<minSet.size();i++){
            System.out.print(vexs.get(minSet.get(i))+" ");
        }
    }
    //求以child为根的树的最小点覆盖集合
    //child:当前正在处理的结点
    //parent:child的父结点
    private void coverSet(int child,int parent){
        minCover[child][0]=1;        //child放入最小点覆盖集合
        minCover[child][1]=0;        //child不放入最小点覆盖集合
        
        for(int i=0;i<vexNum;i++){
            if(edges[child][i]==0 || i==parent)    //如果顶点间不存在边或尾结点为父结点
                continue;
            
            coverSet(i,child);
            
            //如果子结点i放入集合结果更小则把i放入集合
            if(minCover[i][0]<minCover[i][1])
                minCover[child][0]+=minCover[i][0];        //子结点i放入集合
            else
                minCover[child][0]+=minCover[i][1];        //子结点i不放入集合
            
            //若child不放入最小点覆盖集合，则其所有子结点都要放入最小点覆盖集合
            minCover[child][1]+=minCover[i][0];        
            
            if(minCover[child][0]<minCover[child][1])    //取最小值作为结果
                minSet.add(child);        
        }
    }
}