Description
Solution
莫比乌斯反演经典入门题。
题目里面各种推式子的过程也很经典。
话不多说,进入正文。
我们先不管题目,求 \(\sum\limits_{i = 1}^n\sum\limits_{j = 1}^ngcd(i, j)\)
下面就是一波愉快的推式子啦:
\[\sum\limits_{i = 1}^n\sum\limits_{j = 1}^ngcd(i, j)
\]
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^n\sum\limits_{j = 1}^n[gcd(i, j) = k]
\]
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{j = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}[gcd(i, j) = 1]
\]
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{j = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\epsilon(gcd(i, j))
\]
根据 \(\epsilon = \mu * I\),即 \(\epsilon(n) = \sum\limits_{d | n}\mu(d)\),得:
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{j = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | (i, j)}\mu(d)
\]
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{j = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | i}\sum\limits_{d | j}\mu(d)
\]
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | i}\sum\limits_{j = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | j}\mu(d)
\]
我们先考虑这样一个式子如何化简:
\[\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | i}\mu(d)
\]
把枚举 \(i\) 改成枚举 \(d\),\(\left\lfloor\dfrac{n}{k}\right\rfloor\) 以内是 \(d\) 的倍数的数有 \(\left\lfloor\dfrac{n}{dk}\right\rfloor\) 个,得:
\[\sum\limits_{d = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\left\lfloor\dfrac{n}{dk}\right\rfloor\mu(d)
\]
把这个式子代入到刚才我们化简得那个式子中去:
\[\sum\limits_{k = 1}^nk\sum\limits_{i = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | i}\sum\limits_{j = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\sum\limits_{d | j}\mu(d)
\]
\[\sum\limits_{k = 1}^nk\sum\limits_{d = 1}^{ \left\lfloor\frac{n}{k}\right\rfloor}\left\lfloor\dfrac{n}{dk}\right\rfloor^2\mu(d)
\]
至此,我们的式子就推完啦。
但是这道题目还没有结束,因为 \(j\) 的循环是从 \(i + 1\) 开始的,所以还要减去算多的部分。
那么算多了哪些呢?
用一张图来看一下:
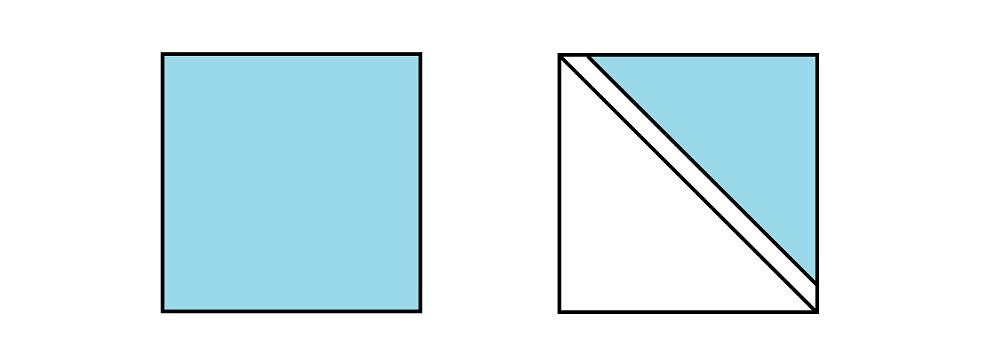
我们式子里计算的是第一张图片中的阴影部分(也就是整个正方形),而这道题目求的第二张图片中的阴影部分(右上角)。
所以答案就是减去对角线再除以二。
对角线上的值是多少呢?
对角线上的点是 \((i, i)\),所以就是 \(\sum\limits_{i = 1}^ngcd(i, i)\),转化一下 \(\sum\limits_{i = 1}^ni\),即\(\frac{n \times (n + 1)}{2}\)。
\[ans = \frac{res - \frac{n \times (n + 1)}{2}}{2}
\]
\(res\) 就是上面式子推出来的值,用整除分块快速求一下即可。
Code
#include <bits/stdc++.h>
#define ll long long
using namespace std;
namespace IO{
inline ll read(){
ll x = 0;
char ch = getchar();
while(!isdigit(ch)) ch = getchar();
while(isdigit(ch)) x = (x << 3) + (x << 1) + ch - '0', ch = getchar();
return x;
}
template <typename T> inline void write(T x){
if(x > 9) write(x / 10);
putchar(x % 10 + '0');
}
}
using namespace IO;
const ll N = 2e6 + 10;
ll n, ans;
ll mu[N], p[N], tot;
bool vis[N];
inline void euler(){
mu[1] = 1;
for(int i = 2; i <= n; ++i){
if(!vis[i]) p[++tot] = i, mu[i] = -1;
for(int j = 1; j <= tot && i * p[j] <= n; ++j){
vis[i * p[j]] = 1;
if(i % p[j] != 0) mu[i * p[j]] = -mu[i];
else{
mu[i * p[j]] = 0;
break;
}
}
}
for(int i = 1; i <= n; ++i) mu[i] += mu[i - 1];
}
inline ll calc(ll n){
ll res = 0;
for(int l = 1, r; l <= n; l = r + 1){
r = min(n, n / (n / l));
res += (mu[r] - mu[l - 1]) * (n / l) * (n / l);
}
return res;
}
signed main(){
n = read();
euler();
for(int k = 1; k <= n; ++k) ans += k * calc(n / k);
write((ans - (n * (n + 1) >> 1)) >> 1), puts("");
return 0;
}
\[\_EOF\_
\]