机器学习之逻辑回归

一、二分类逻辑回归模型

逻辑回归是一种分类模型，由条件概率分布$P(Y|X)$表示，形式为参数化的逻辑分布。随机变量$X$的取值为 实数，随机变量$Y$的取值为0或1。通过监督学习的方法来估计参数模型。

对于二分类任务，逻辑回归模型为如下的条件概率：

$P(Y=1|x)=frac{e^{wcdot x+b}}{1+e^{wcdot x+b}}$                          （1）

$P(Y=0|x)=frac{1}{1+e^{wcdot x+b}}$                          （2）

其中，$Xin mathbb{R}^{n}$是输入，$Yinleft { 0,1 ight }$是输出，$win mathbb{R}^{n}$和$win mathbb{R}^{n}$是参数。$w$称为权重向量，$b$为偏置。对于给定的输入实例$x$，由式（1）和式（2）可以求得$P(Y=1|x)$和$P(Y=0|x)$。

逻辑回归就是比较这两个概率值得大小，将实例$x$分到概率值较大的那一类。

为了公式推导方便，可以将偏置项扩充到权重向量中，仍记作$w$，$x$，即$w=(w^{(1)},w^{(2)},...,w^{(n)},b)^{T}$，$x=(x^{(1)},x^{(2)},...,x^{(n)},1)^{T}$。此时，逻辑回归模型可以如下表示：

$P(Y=1|x)=frac{e^{wcdot x}}{1+e^{wcdot x}}$                              (3)

$P(Y=0|x)=frac{1}{1+e^{wcdot x}}$                              (4)

二、几率

事件的几率是指该事件发生的概率与不发生的概率的比值。如果事件发生的概率为$p$，那么该事件的几率是$frac{p}{1-p}$，该事件的对数几率或logit函数为：

$logit(p)=logfrac{p}{1-p}$

将式（3）、（4）带入得到

$logit(p)=logfrac{P(Y=1|x)}{1-P(Y=1|x)}=wcdot x$

即对于逻辑回归模型，输出Y=1的对数几率是x的线性函数。

从另一个角度，考虑对输入$x$进行分类的线性函数$wcdot x$，其值域为实数域。通过逻辑回归模型可以将线性函数$wcdot x$转换成概率：

$P(Y=1|x)=frac{e^{wcdot x}}{1+e^{wcdot x}}$

此时，线性函数的值越接近正无穷，概率值越接近1；线性函数的值越接近负无穷，概率值接近0（sigmoid函数）。

三、模型参数估计

逻辑回归模型学习时，对于给定的训练数据$T=left { (x_{1},y_{1}),(x_{2},y_{2},...,(x_{N},y_{N})) ight }$，其中，$x_{i}in mathbb{R}^{n}$，$y_{i}in left { 0,1 ight }$，可以使用极大似然估计法估计模型参数，从而得到逻辑回归模型。

假设：

$P(Y=1|x)=pi (x),P(Y=0|x)=1-pi (x)$

似然函数为：

$prod_{i=1}^{N}left [ pi (x) ight ]^{y_{i}}left [ 1-pi (x) ight ]^{1-y_{i}}$

对数似然函数为：

$L(w)=sum_{i=1}^{N}left [ y_{i}logpi (x_{i})+(1-y_{i})log(1-pi (x_{i})) ight ]$

         $=sum_{i=1}^{N}left [ y_{i}logfrac{pi (x_{i})}{1-pi (x_{i})}+log(1-pi (x_{i})) ight ]$
         $=sum_{i=1}^{N}left [ y_{i}(wcdot x_{i})-log(1+e^{wcdot x_{i}}) ight ]$

对$L(w)$求极大值，得到$w$的估计值。这样问题就变成了以对数似然函数为目标函数的最优化问题。逻辑回归模型通常采用的方法是梯度下降算法和拟牛顿法。

假设$w$的极大似然估计值为$hat{w}$，那么学习到的逻辑回归模型为：

$P(Y=1|x)=frac{e^{hat{w}cdot x}}{1+e^{hat{w}cdot x}}$

$P(Y=0|x)=frac{1}{1+e^{hat{w}cdot x}}$

对对数似然函数求梯度：

$frac{partial L(w)}{partial w}=sum_{i=1}^{N}left [ y_{i}x_{i}-frac{1}{1+e^{wcdot x_{i}}}cdot e^{wcdot x_{i}}cdot x_{i} ight ]$

$=sum_{i=1}^{N}left [ y_{i}x_{i}- h(x_{i})x_{i} ight ]$

$=sum_{i=1}^{N}left [ (y_{i}- h(x_{i}))x_{i} ight ]$

$=sum_{i=1}^{N}error_{i}cdot x_{i}$

 $=mathbf{x}cdot mathbf{error}$

四、实践

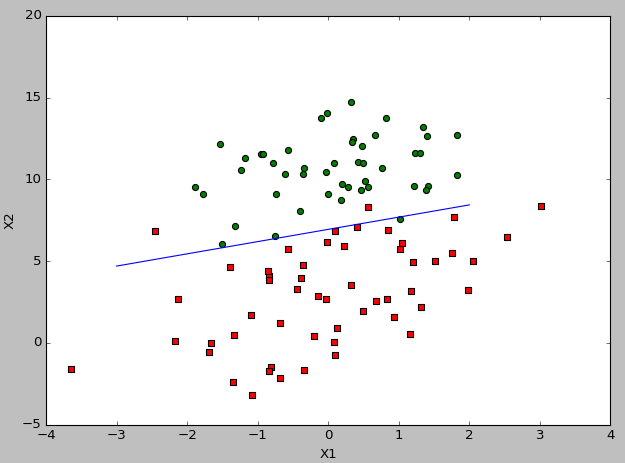
import numpy as np

def loadDataSet():
    dataMat=[]
    labelMat=[]
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat


def sigmoid(inX):
    return 1.0/(1+np.exp(-inX))


def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)
    labelMat = np.mat(classLabels).transpose()
    m,n = np.shape(dataMatrix)
    alpha = 0.001
    maxCycles = 100000
    weights = np.mat(np.ones((n,1)))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)   # m*1
        error = labelMat - h              # m*1 -m*1
        weights = weights+alpha*dataMatrix.transpose()*error  # n*m-m*1-->n*1
    return weights

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat, labelMat = loadDataSet()
    dataArr = np.array(dataMat)
    n = np.shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1]); ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = np.arange(-3.0, 3.0, 1)
    y = (-float(weights[0])-float(weights[1])*x)/float(weights[2])
    # y = (-weights[0] - weights[1] * x) / weights[2]
    ax.plot(x, y)
    plt.xlabel('X1'); plt.ylabel('X2')
    plt.show()

dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
plotBestFit(weights)

实验结果：