题目:最大连续子数组和(最大子段和)
问题: 给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的
最 优值为 : Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
1.方案论证
给定一组包含负数的整数,求出其中最大的连续的子数组的和。
其实本小白看到这里,第一反应就是--枚举法。
(1)枚举?
对,枚举是万能的!枚举什么?子数组的位置!
好枚举一个开头位置i,一个结尾位置j>=i,再求a[i...j]之间所有数的和,找出最大的就可以啦!
但是,就在准备写代码的时候,我眼疾手快地百度了一番,最后,本小白发现,竟然有四种方法可以解决最大子段和!哪四种呢?
第一种自然就是最容易想到也最容易明白且最暴力的枚举法;
第二种则是将枚举法进行算法优化的分治法;
第三种则是根据第二种的分治法再进行进一步的算法优化而得的动态规划法(DP);
第四种则是需要常量空间并以线性时间运行的联机算法;
在此,本小白来捡一捡之前丢过的苞米吧!
何为算法优化?
这算法优化是指对算法的有关性能进行优化,如时间复杂度、空间复杂度、正确性、健壮性。大数据时代到来,算法要处理数据的数量级也越来越大以及处理问题的场景千变万化。为了增强算法的处理问题的能力,对算法进行优化是必不可少的。算法优化一般是对算法结构和收敛性进行优化。(哎呀,苞米捡没捡起来只有自己知道啊!)
那么重点来了!时间复杂度!空间复杂度!......
在第一种方法枚举法当中,好的,时间复杂度:
①枚举i,O(n)
②枚举j,O(n)
③求和a[i...j],O(n)
大致算法如下:
for(int i = 1; i <= n; i++)
{
for(int j = i; j <= n; j++)
{
int sum = 0;
for(int k = i; k <= j; k++)
sum += a[k];
max = Max(max, sum);
}
}
所以总时间复杂度是O(n^3)
那么在对枚举法稍稍优化一下呢?降低一下时间复杂度呢?仍然是枚举! 能不能在枚举的同时计算和?
①枚举i,O(n)
②枚举j,O(n) ,这里面,诶?a[i...j]的和不就是a[i...j – 1]的和加上a[j]么?所以,当j+1的时候把a[j]加到之前的结果上不就可以了吗?那么这样,便可以得到一个时间复杂度为O(n^2)的算法。
大致算法如下:
for(int i = 1; i <= n; i++)
{
int sum = 0;
for(int j = i; j <= n; j++)
{
sum += a[j];
max = Max(max, sum);
}
}
(2)那么又何为分治呢?
将数组分开治理?
针对最大子段和这个具体问题本身的结构,还可以从算法设计的策略上对上述O(n^2)计算时间算法进行更进一步的改进。从中间将数组一分为二,原数组的最大子段和要么是两个子数组的最大子段和, 要么是跨越中心分界点的最大子段和。
如果将所给的序列a[1:n]分为长度相等的两段a[1:n/2]和a[n/2+1:n],分别求出这两段的最大子段和,则a[1:n]的最大子段和的三种情况便是:
(1) a[1:n]的最大子段和与a[1:n/2]的最大子段和相同
(2) a[1:n]的最大子段和与a[n/2+1:n]的最大子段和相同
(3) a[1:n]的最大子段和为a[i]+…+a[j],并且1<=i<=n/2,n/2+1<=j<=n。
对于(1)和(2)两种情况可递归求得,但是对于情况(3),容易看出a[n/2],a[n/2+1]在最大子段中。因此,我们可以在a[1:n/2]中计算出s1=max(a[n/2]+a[n/2-1]+…+a[i]),0<=i<=n/2,并在a[n/2+1:n]中计算出s2= max(a[n/2+1]+a[n/2+2]+…+a[i]),n/2+1<=i<=n。则s1+s2为出现情况(3)的最大子段和。
于是算法变成了:
①拆分子数组分别求长度近乎一半的数组的最大子段和s1, s2:时间复杂度 2* T(n / 2)
②从中心点往两边分别分别找到最大的和,找到跨越中心分界点的最大子段和s3 :时间复杂度 O(n)
那么总体时间复杂度是T(n) = 2 * T(n / 2) + O(n) = O(nlogn)。
那么还能在优化?
(3)动态规划?
动态规划,其实本小白并不懂是什么,但是还是多亏了CSDN上的大神啊!(鉴于已经找不到扔到角落里长毛的CSDN账号,我还重新注册了另一个账号!)
在对于上述分治算法的分析中,若记b[j]=max(a[i]+a[i+1]+..+a[j]),其中1<=i<=j,并且1<=j<=n。则所求的最大子段和为max b[j],1<=j<=n。
由b[j]的定义可易知,当b[j-1]>0时b[j]=b[j-1]+a[j],否则b[j]=a[j]。故b[j]的动态规划递归式为:b[j]=max(b[j-1]+a[j],a[j]),1<=j<=n。则时间复杂度为O(n)。
大致算法如下:
for(i=1; i<n; i++)
{
if(b[i-1]>0)
b[i]=b[i-1]+a[i];
else
b[i]=a[i];
if(b[i]>max)
max=b[i];
}
(4)联机算法?
联机算法是在任意时刻算法对要操作的数据只读入(扫描)一次,一旦被读入并处理,它就不需要在被记忆了。而在此处理过程中算法能对它已经读入的数据立即给出相应子序列问题的正确答案。求一个序列的最大子段和,从头到尾遍历一次,存放当前最大值和总和,总和小于0(当所给的整数均为负数时定义子段和为0)则将其定义为0。
int maxSum(int array[],int n)
{
int thissum=0,maxsum=0;
for(int i=0;i<n;i++){
thissum+=array[i];
if(thissum<0)
thissum=0;
else if(thissum>maxsum)
maxsum=thissum;
}
return maxsum;
}
用Eclipse实现代码的编写以及测试。
2.代码输入
代码管理coding.net
(1)求和代码

(2)测试代码
用Junit4自动测试
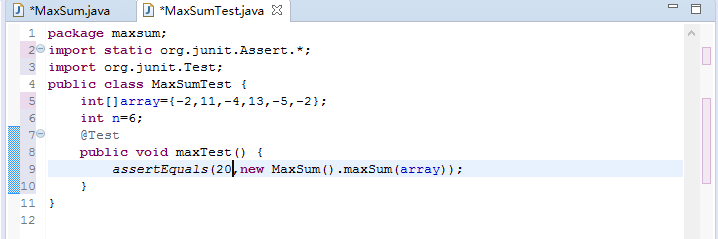
以题目所给数据进行代码自动测试,为覆盖测试做准备。覆盖测试仅更换数据即可。

3.覆盖测试
覆盖测试选择:条件组合覆盖
覆盖标准:使得每个判定中条件的各种可能组合都至少出现一次。
(1)主要程序流程图
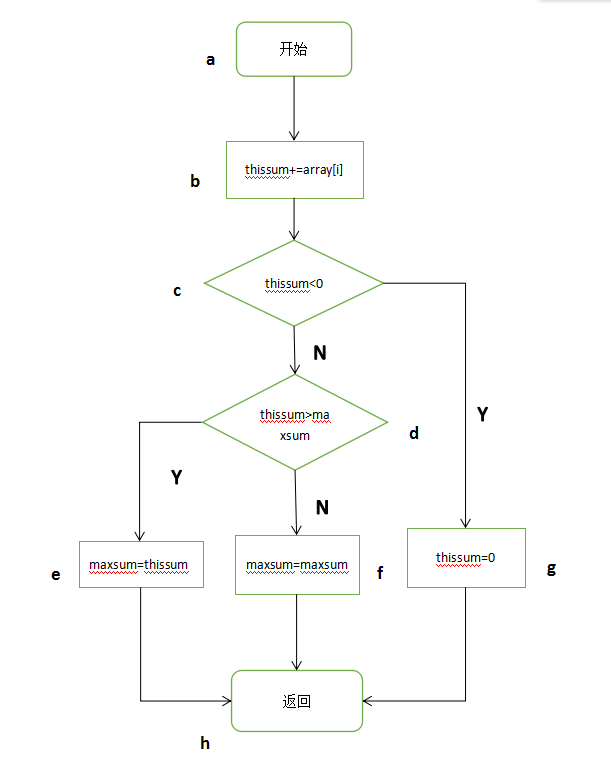
(2)条件组合以及相关路径覆盖

(3)条件组合覆盖
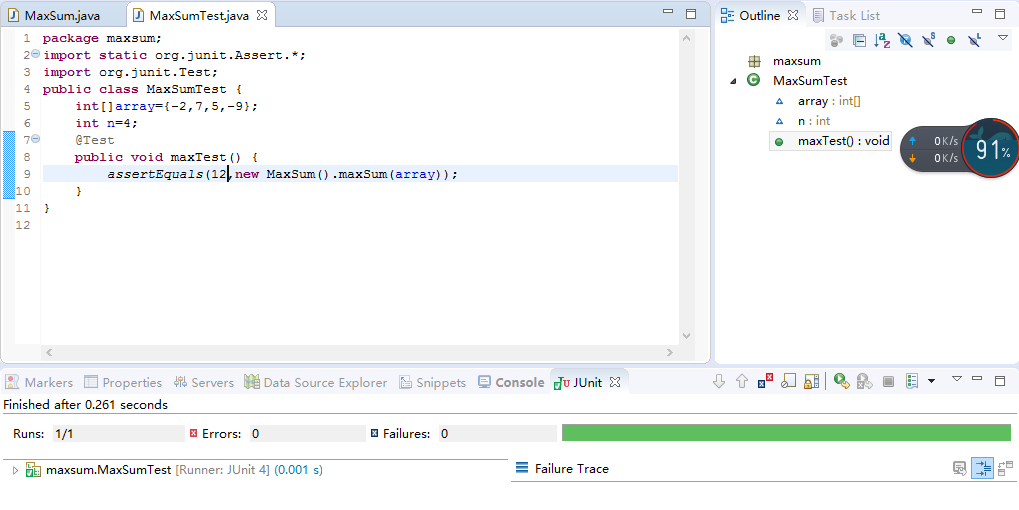
①测试用例:{-2,7,5,-9}
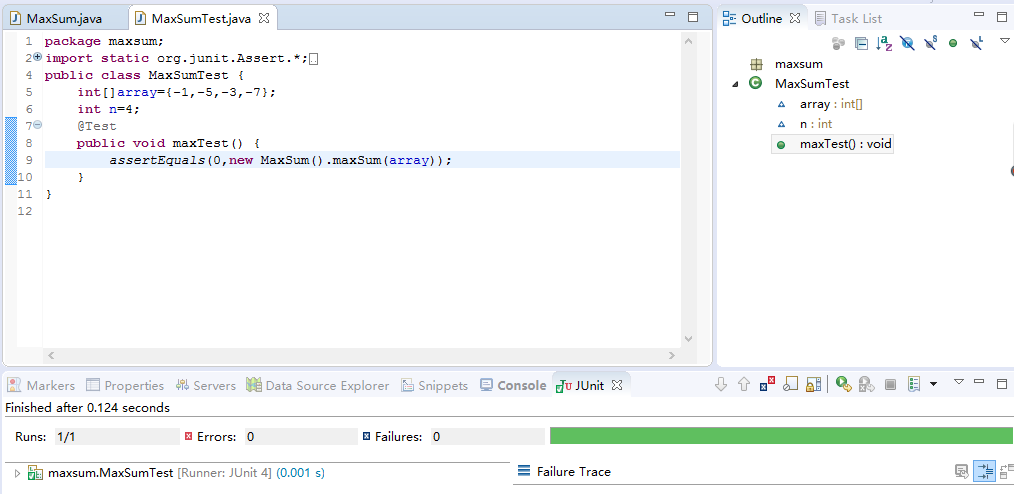
②测试数组全为负数情况:{-1,-5,-3,-7}
这就结束啦!真是猝不及防!