已知$vartriangle ABC$的面积为$1$,$D,E$分别是边$AB,AC$上的点,$F$为线段$DE$上的一点,设$AD:AB=x$,$AE:AC=y$,$DF:DE=z$且$y+z-x=1$.求$vartriangle BDF$的面积的最大值并求出此时$x,y,z$的值.
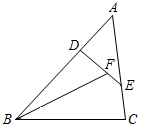
解:如图,连结$BE$:
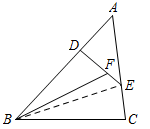
由三角形的面积公式$S=dfrac{1}{2}absin C$可以得到
${{S}_{vartriangle ADE}}=xy{{S}_{vartriangle ABC}}=xy$,${{S}_{vartriangle BCE}}=(1-y){{S}_{vartriangle ABC}}=1-y$,
所以有${{S}_{vartriangle BCD}}=1-xy-(1-y)=y(1-x)$,
从而有${{S}_{vartriangle BDF}}=z{{S}_{vartriangle BDE}}=zy(1-x)$$le {{left( dfrac{z+y+1-x}{3} ight)}^{3}}=dfrac{8}{27}$.
当$y=z=1-x$时,即$x=dfrac{1}{3}$,$y=z=dfrac{2}{3}$时等号成立,
此时$vartriangle BDF$的面积有最大值$dfrac{8}{27}$.