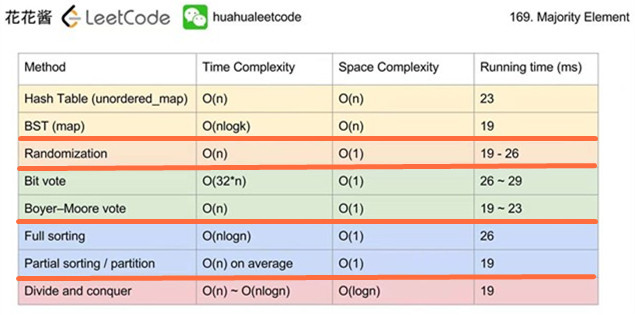
169_求众数(Majority-Element)
这道题有 5 种方法,8 种实现,详细分析可以看花花酱的 YouTube 专栏。
目录
描述
给定一个大小为 n 的数组,找到其中的众数。众数是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在众数。
示例 1:
输入: [3,2,3]
输出: 3
示例 2:
输入: [2,2,1,1,1,2,2]
输出: 2
解法一:暴力法
思路
遍历数组中的每个元素,统计该元素出现的次数(嵌套遍历),如果该元素出现的次数 (> left lfloor n/2 ight floor),则该元素就是数组的众数。
Java 实现
class Solution {
public int majorityElement(int[] nums) {
int majorityCount = nums.length / 2;
for (int num1 : nums) {
int count = 0;
for (int num2 : nums) {
if (num2 == num1) {
++count;
}
}
if (count > majorityCount) {
return num1;
}
}
throw new IllegalArgumentException("The array does not contain a majority element!");
}
}
Python 实现
class Solution:
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
majority_count = len(nums) // 2
for num1 in nums:
count = sum(1 for num2 in nums if num2 == num1)
if count > majority_count:
return num1
复杂度分析
- 时间复杂度:(O(n^2)),其中 (n) 表示数组的长度,由于嵌套了两层
for循环,因此总的时间复杂度是 (O(n^2)) 的 - 空间复杂度:(O(1))
解法二:哈希表
思路
利用哈希表记录数组中元素出现的次数,由于哈希表的插入操作的时间复杂度是 (O(1)) 的,所以遍历整个数组统计出现次数的操作的时间复杂度是 (O(n)) 的。接着,再遍历一遍哈希表,取出众数。
Java 实现
class Solution {
public int majorityElement(int[] nums) {
Map<Integer, Integer> counts = new HashMap<>();
for (int num : nums) {
if (counts.containsKey(num)) {
counts.replace(num, counts.get(num) + 1);
} else {
counts.put(num, 1);
}
}
Map.Entry<Integer, Integer> majorityEntry = null;
for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()) {
majorityEntry = entry;
}
}
return majorityEntry.getKey();
}
}
Python 实现
class Solution:
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
counts = dict()
for num in nums:
counts[num] = counts.get(num, 0) + 1
return max(counts, key=counts.get)
复杂度分析
- 时间复杂度:(O(n)),其中 (n) 为数组的长度。由于哈希表中元素的数目最多为 (n - left( left lfloor n/2 ight floor + 1 ight) + 1 = n - left lfloor n/2 ight floor),因此遍历一次哈希表最多需要 (n - left lfloor n/2 ight floor) 次操作,而遍历一遍数组需要 (n) 次操作,所以总的时间复杂度是 (O(n)) 的
- 空间复杂度:(O(n)),因为哈希表最多需要保存 (n - left lfloor n/2 ight floor) 个元素
解法三:排序
将数组按照顺序(递增或者递减)排列好后,索引为 (left lfloor n/2 ight floor) 的元素就是数组的众数。
Java 实现
class Solution {
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length / 2];
}
}
Python 实现
class Solution:
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return sorted(nums)[len(nums) // 2]
复杂度分析
- 时间复杂度:(O(n log(n))),其中 (n) 表示数组的长度,对数组进行排序的时间复杂度为 (O(n log(n))) 的
- 空间复杂度:(O(n)) 或者 (O(1)),取决于是否可以直接对原数组直接进行排序,如果不允许的话,需要额外的空间复制数组
解法四:随机选择【待完成】
思路
Java实现
Python 实现
复杂度分析
解法五:分而治之(Divide and conquer)【待完成】
思路
Java 实现
Python 实现
复杂度分析
解法六:多数投票算法(Boyer-Moore majority vote algorithm)
思路
多数投票算法一般用于寻找一个序列的多数元素(只需要线性时间和常数空间),是一种典型的流式算法(streaming algorithm)。但是,一般来说,该算法无法找到一个序列的众数(mode),除非众数出现的次数大于 (lfloor n/2
floor) 次。多数投票算法的思想是这样:统计一个序列中的所有元素,将多数元素记为 (+1),其余的元素记为 (-1),那么最后的和一定是正的。具体地,该算法会维护两个变量,一个用于记录序列中的元素,记为 m,一个作为计数器,记为 count。遍历数组中的每个元素,如果当前的 count 为 0,则将当前元素保存在 m 中,并设 count 为1;如果 count 不为0,则判断当前元素与 m 是否相等,相等则 count 加一,不等则 count 减一。遍历结束,变量 m 就是我们寻找的多数元素。
Java 实现
class Solution {
public int majorityElement(int[] nums) {
int me = nums[0], count = 1;
for (int i = 1; i < nums.length; ++i) {
if (count == 0) {
me = nums[i];
count = 1;
} else if (me == nums[i]) {
++count;
} else {
--count;
}
}
return me;
}
}
Python 实现
class Solution:
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
me, count = 0, 0
for num in nums:
if count == 0:
me, count = num, 1
elif me == num:
count += 1
else:
count -= 1
return me
复杂度分析
- 时间复杂度:(O(n)),其中 (n) 表示数组的长度
- 空间复杂度:(O(1))