题目描述
每年的 1024 程序员节日,黑马程序员都会举办大型的庆祝活动。今年的程序员节也不例外,每个班级的同学都发了橙子。
班级里有 n 名同学从前到后排成一排,且已经得知了这些同学的成绩,其中第 i名同学的成绩是 ai。班主任想根据同学们上个阶段的考试成绩来评定发橙子的数量。为了激励成绩优秀同学,发橙子时需要满足如下要求:
- 相邻同学中成绩好的同学的橙子必须更多。若相邻的同学成绩一样,则它们分到的数量必须平等。
- 每个同学至少分配一个橙子
由于预算有限,班主任希望在符合要求的情况下发出尽可能少的橙子。请问,至少需要准备多少橙子呢?
输入格式
第一行是一个不超过 10^6正整数 n,表示学生数量。
接下来一行有 n 个不超过 10^9 的非负整数 ai,表示第 i 个同学的成绩。
输出格式
输出答案,也就是需要最少准备多少个橙子。
输入样例:
11
3 6 9 4 7 7 2 13 15 15 19
输出样例:
24
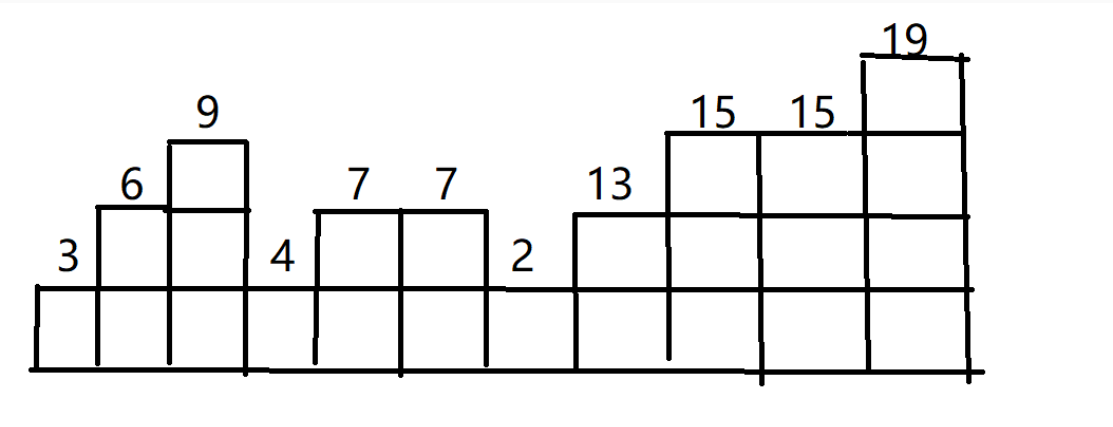
思路:这是一个正向和反向的不减子列,初始化每个人有一个橘子,接着遍历数组,后一个比前一个成绩高,则橘子也多一,接着反向再遍历一遍数组,也是求不减子列,最后累加数组求和。
#include <cstdio> #include <string.h> #include <iostream> #include <algorithm> #include <sstream> #include <math.h> #include <map> using namespace std; const int inf=999999;//0x7fffff const long long mod=1e9+7; const double PI=acos(-1); long long n,m; long long ans=0; bool vis[105]; long long dis[10000000],get[10000000]; int main() { cin>>n; for(int i=1;i<=n;i++){ cin>>dis[i]; get[i]=1; //初始化get数组,因为每个学生最少有1个橘子 } for(int i=2;i<=n;i++){ //从左向右扫一遍数组,相当于从左向右寻找不减子列 if(dis[i]>dis[i-1]){ // 如果后一个学生分数大于前一个学生 橘子数也比前一个学生橘子多一个 get[i]=get[i-1]+1; } else if(dis[i]==dis[i-1]){ //分数相等橘子数也应该相等 get[i]=get[i-1]; } } for(int i=n-1;i>=1;i--){ //接着再从右向左扫一遍数组,也是从右向左找不减子列 if(dis[i]>dis[i+1]){ get[i]=max(get[i],get[i+1]+1); // 同样的,成绩高的比旁边成绩低的橘子数多一个 但要考虑第一次排序结果,所有取此次结果和上一次结果的较大者 } else if(dis[i]==dis[i+1]){ //分数相等橘子数也应该相等 get[i]=get[i+1]; } } for(int i=1;i<=n;i++){ //累加求橘子数 ans+=get[i]; } cout<<ans; return 0; }