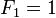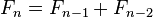面试题9：斐波那契数列

题目1：写一个函数，输入n，其斐波那契数列的第n项。

斐波那契数列的定义如下：

• 
• 
• 

方法1：使用递归解，时间复杂度是n的指数级别

斐波那契数列的定义就是递归的，我们根据定义可以很简单的写出代码。代码如下：

#include<iostream>
#include<stdlib.h>
using namespace std;

//f(n)={0,1,1,2,3...} n>=0

int Fibonacci(int n)
{
    if(n<=0)
        return 0;
    if(n==1)
        return 1;
    return Fibonacci(n-1)+Fibonacci(n-2);
}

void main()
{
    int f=Fibonacci(30);
    cout<<f<<endl;

    system("pause");
}

但是这样的方法存在明显的不足，该方法的时间复杂度是n的指数级别，随着n的增大，运算时间不可想象，比如说f(50)就要很久。时间复杂度之所以这么大，是因此计算过程中存在着重复计算。以f(10)为例，f(10)=f(9)+f(8)，f(9)=f(8)+f(7)。其中的f(8)就是重复计算的。

方法2：开辟一个长度为(n+1)的数组，时间复杂度为O(n)，空间复杂度为O(n)

前面我们计算斐波那契数列是从后往前计算的，就是计算f(n)=f(n-1)+f(n-2)，然后再递归计算f(n-1)，又是从后往前计算，就是因为这样的从后往前计算，所以才会有很多的重复计算。那么我们可以逆转思路，考虑从前往后计算。比如我们要计算f(4)，那么我们就计算f(0)、f(1)、f(2)、f(3)，将这些计算出来的值保存在一个数组arry[n+1]上，这样计算斐波那契数列就相当于是一个填表的过程。时间复杂度大大降低。代码实例如下:

int Fibonacci(int n)
{
    if(n<=0)
        return 0;
    else if(n==1)
        return 1;
    else
    {
        //动态创建一个长度为(n+1)的数组
        int *arry=new int[n+1];
        arry[0]=0;
        arry[1]=1;
        for(int i=2;i<=n;i++)
        {
            arry[i]=arry[i-1]+arry[i-2];
        }
        int result=arry[n];
        //因为动态创建的数组不会因为出了作用域，内存就会被释放。
        //动态分配的数组将一直存在，直到程序显示释放它为止，因此这里使用delete []
        //c++提供delete []表达式释放指针所指向的数组空间。
        delete [] arry;
        return result;
    }
}

注意点：

1. 因为不知道要求的f(n)中的n有多大，因此不能事先开辟一个数组，需要动态创建数组。而动态数组与数组变量不同，动态分配的数组将一直存在，直到程序显式释放它为止。普通的数组变量，只要出了数组的作用于，其内存会自动释放。
2. c++提供delete []表达式释放指针所指向的数组空间。delete [] arry;该语句回收了arry所指向的数组，把相应的内存返回给自由存储区。在关键字delete和指针arry之间的方括号[]是必不可少的：它告诉编译器该指针指向的是自由存储区中的数组，而非单个对象。delete arry只释放了arry指针所指向的内存地址，理论上来说会少释放了内存空间，从而产生内存泄露。

方法3：优化方法2，空间复杂度为O(1)，时间复杂度为O(n)

在方法2中，我们保存了每一个中间变量，但是仔细观察我们可以发现没有必要保存每一个中间变量，我们只需要保存两个临时变量即可完成斐波那契数列的计算。具体代码试下如下：

int Fibonacci(int n)
{
    if(n<=0)
        return 0;
    else if(n==1)
        return 1;

    else
    {
        //当n>=2时，初始化pre=f(0)=0,post=f(1)=1,f(n)=0;
        int pre=0;
        int post=1;
        int fn=0;
        //采用循环计算斐波那契数列，通过两个临时变量pre和post保存中间结果，避免重复计算
        for(int i=2;i<=n;i++)
        {
            fn=pre+post;//fn等于其前面两个元素值的和
            //然后让pre和post分别直线他们后面的元素。
            pre=post;
            post=fn;
        }
        return fn;
    }
}

题目2：一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。

这道题目的本质就是斐波那契数列。假设只有一个台阶，那么只有一种跳法，那就是一次跳一级，f(1)=1；如果有两个台阶，那么有两种跳法，第一种跳法是一次跳一级，第二种跳法是一次跳两级,f(2)=2。如果有大于2级的n级台阶，那么假如第一次跳一级台阶，剩下还有n-1级台阶，有f(n-1)种跳法，假如第一次条2级台阶，剩下n-2级台阶，有f(n-2)种跳法。这就表示f(n)=f(n-1)+f(n-2)。将上面的斐波那契数列代码稍微改一下就是本题的答案。这列略之。

题目3：我们可以用2X1（2行1列）的小矩形横着或者竖着去覆盖更大的矩形。请问用8个2X1的小矩形无重复地覆盖一个2X8的大矩形，总共有多少种方法。

 这道题目还是斐波那契数列的变种。设f(8)表示覆盖2X8大矩形的方法综述。假设第一个小矩形是竖着去覆盖大矩形，那么还剩下由7个2X1的小矩形组成的大矩形f(7)；假设第一个小矩形是横着去覆盖大矩形，那么还剩下由6个2X1的小矩形组成的大矩形f(6)。即f(8)=f(7)+f(6)。依此类推，最后f(1)=1，f(2)=2。使用计算斐波那契数列的方法计算这道题目即可求出答案。