题目描述
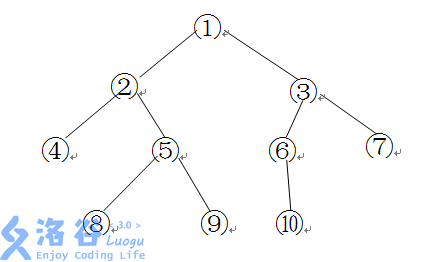
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为:
深度:4 宽度:4(同一层最多结点个数)
结点间距离: ⑧→⑥为8 (3×2+2=8)
⑥→⑦为3 (1×2+1=3)
注:结点间距离的定义:由结点向根方向(上行方向)时的边数×2,
与由根向叶结点方向(下行方向)时的边数之和。
输入格式
输入文件第一行为一个整数n(1≤n≤100),表示二叉树结点个数。接下来的n-1行,表示从结点x到结点y(约定根结点为1),最后一行两个整数u、v,表示求从结点u到结点v的距离。
输出格式
三个数,每个数占一行,依次表示给定二叉树的深度、宽度及结点u到结点v间距离。
输入输出样例
输入 #1
10
1 2
1 3
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6
输出 #1
4
4
8
题解思路:
原本的打算是先建立一棵树,再进行dfs。但对于此题,已经知道根节点始终是1且各节点连接信息表现出来的情况下,可以直接利用邻接矩阵+dfs从根节点搜,保存各节点的深度信息即可。
具体步骤如下:
1.先使用邻接矩阵(即二维数组)储存各节点长度关系,如a[i][j]储存第i和第j个结点的距离,若两节点不连接,则设置为0。
2.首先,从根节点(1)开始往下搜,用dfs遍历所有的结点,在遍历的同时用depth数组储存各节点的深度,如根节点1的深度为1,每访问到一个节点就保存深度信息。
3.有了结点信息后,进行排序求出最大深度。另外,通过统计相同的深度的节点数量即可确定树的最大宽度。
4.接下来,开始对起始要搜索的点dfs,当碰见一个节点,进行深度比较,若深度大于该节点则路程加2,若小于该节点则路程加1,知道遇到终止点。、
代码:
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 using namespace std; 5 6 //原本的打算是先建立一棵树,再进行dfs 7 //但对于此题,已经知道根节点始终是1且各节点连接信息表现出来的情况下,可以直接利用邻接矩阵+dfs从根节点搜,保存各节点的深度信息即可 8 #define INF 999999999 9 int depth[101]; //记录各节点的深度信息 10 int broad[100]; //记录宽度(dfs后记录) 11 int map[101][101]={0}; //邻接矩阵,0代表无连接,1代表连接 12 int n=0; 13 int flag[101]={0}; //存储各节点是否被访问的信息 14 int u=0,v=0; //起始和目标 15 int minsum=INF; 16 17 bool cmp(int a,int b){ 18 return a>b; 19 } 20 void dfs(int cur,int dep){ 21 flag[cur]=1; 22 depth[cur]=dep; 23 // cout<<"cur:"<<cur<<" depth:"<<depth[cur]<<endl; 24 25 for(int i=1;i<=n;i++){ 26 if(flag[i]==1) continue; //防止来回搜死循环 27 if(map[cur][i]!=0){ 28 dfs(i,dep+1); 29 } 30 flag[i]=0; //回溯 31 } 32 return ; 33 } 34 void dfs1(int cur,int sum){ //cur是结点编号,sum为当前距离 35 // cout<<"cur:"<<cur<<" sum:"<<sum<<endl; 36 flag[cur]=1; 37 if(sum>=minsum){ 38 return ; //剪枝 39 } 40 if(cur==v){ 41 if(sum<minsum){ 42 minsum=sum; 43 } 44 return; //找到并返回,更新minsum 45 } 46 47 for(int i=1;i<=n;i++){ 48 if(flag[i]==1) continue; 49 if(map[cur][i]!=0){ 50 if(depth[i]>depth[cur]){ 51 dfs1(i,sum+1); //向下搜 52 }else if(depth[i]<depth[cur]){ 53 dfs1(i,sum+2); //向上搜 54 } 55 } 56 flag[i]=0; //回溯 57 } 58 59 return; 60 } 61 int main(){ 62 cin>>n; 63 for(int i=1;i<=n-1;i++){ 64 int m,k; 65 cin>>m>>k; 66 map[m][k]=map[k][m]=1; 67 } 68 cin>>u>>v; 69 70 dfs(1,1); 71 int maxdepth=0; //最大深度 72 int maxbroad=0; //最大宽度 73 for(int i=1;i<=n;i++){ 74 if(depth[i]>maxdepth){ 75 maxdepth=depth[i]; 76 } 77 broad[depth[i]]++; //同一深度的结点数量累加 78 } 79 sort(broad,broad+n,cmp); 80 maxbroad=broad[0]; 81 82 //上述进行完树的深度和宽度查询后,下面开始距离搜索 83 memset(flag,0,sizeof(flag)); 84 dfs1(u,0); 85 cout<<maxdepth<<endl<<maxbroad<<endl<<minsum; 86 return 0; 87 }