图的m着色问题

问题描述

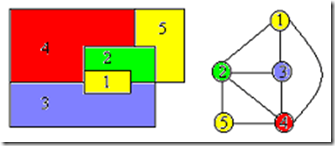
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。

给定图G=(V,E)和m种颜色，如果这个图不是m可着色，给出否定回答；如果这个图是m可着色的，找出所有不同的着色法。

问题分析

1> 解向量：(x1, x2, … , xn)表示顶点i所着颜色x[i]

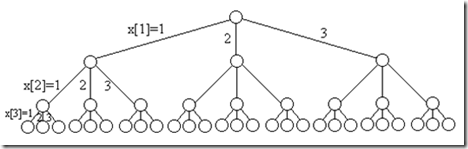
2> 解空间树：子集树，下图为n=3,m=3时问题的解空间树

3> 剪枝函数：顶点i与已着色的相邻顶点颜色不重复。约束函数

算法实现

/** 
图的m着色问题
输入示例
5 8 5
1 2
1 3
1 4
2 3
2 4
2 5
3 4
4 5
*/
#include <iostream>
using namespace std;

class Color
{
	friend int mColoring(int,int,int**);
	private:
		bool ok(int k);
		void backtrack(int t);
		int n,			// 图的顶点数
			m,			// 可用颜色数 
			**a,		// 图的邻接矩阵
			*x,			// 当前解
			sum;		// 当前已找到的可m着色方案数
};

bool Color::ok(int k)
{
	// 检查颜色可用性
	for (int j=1; j<k; j++)
	{
		if ((a[k][j]==1)&&(x[j]==x[k]))
			return false;
	}
	return true;
}

/* 回溯法 子集树 */
void Color::backtrack(int t)
{
	if (t>n)	// 搜索到叶子结点
	{
		sum++;
		for (int i=1; i<=n; i++)
		{
			cout << x[i] << " ";
		}
		cout << endl;
	}
	else
	{
		for (int i=1; i<=m; i++)
		{
			x[t] = i;
			if (ok(t))
			{
				backtrack(t+1);
			}
			x[t] = 0;
		}
	}
}

int mColoring(int n, int m, int** a)
{
	Color C;
	// 初始化C
	C.n = n;
	C.m = m;
	C.a = a;
	C.sum = 0;
	int *x = new int[n+1];
	for (int i=0; i<=n; i++)
	{
		x[i] = 0;
	}
	C.x = x;
	C.backtrack(1);
	delete []x;
	return C.sum;
}

void main()
{
	int e,m,n,u,v;

    int** a = new int*[100];
    for(int k=0; k<100; k++)
	{
        a[k] = new int[100];
	}

	while(1)
	{
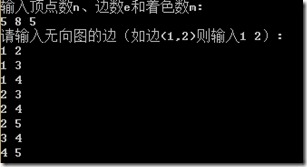
		cout << "输入顶点数n、边数e和着色数m:" << endl;
		cin >> n >> e >> m;
		cout << "请输入无向图的边（如边(1,2)则输入1 2）:" << endl;
		for (int i=0; i<e; i++)
		{
			cin >> u >> v;
			a[u][v] = 1;
			a[v][u] = 1;
		}
		cout << "可行的着色法:" << endl;
		int sum = mColoring(n,m,a);
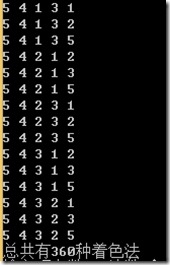
		cout << "总共有" << sum << "种着色法" << endl;
	}
}

程序执行结果：