最优边界分类器（最大间隔分类器）(续学习笔记五)
在线性分类器中，我们要找到一个边界线，使得几何间隔最大，即：
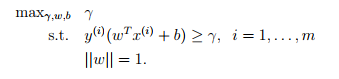||w||在几何间隔中是无关紧要的，这里取1，使得几何间距和函数间距一致。
但是这个并不是一个凸函数最优求解问题，无法使用求解软件进行求解。下面进行变形，首先先将几何间距化为函数间距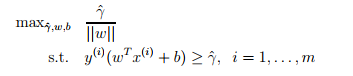
，由于几何间距是函数间距的化归后的结果，所以函数间距可以取任意值而不影响最后结果，所以另函数间距为1，那么又可以将其变形为
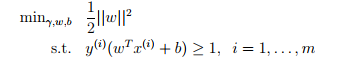。通过这样的转化，就可以使用二元规划（QP）方式进行求解。
拉格朗日对偶（Lagrange duality）
假如想进行一下问题求解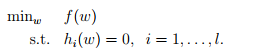
，可以构造lagrange算子，
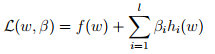，beta称为lagrange乘数，进行以下运算，
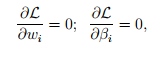，就可以解决要求解的问题了。
原始问题(primal optimization problem)
此时的lagrange算子变成了
。
定义
。如果违反了原始问题的任意一个约束，那么原始问题的结果就变成了无穷大。所以可以写成
，所以
就是原始问题的求解了。同时定义
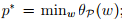
对偶问题(dual problem)
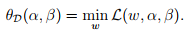对偶优化问题即为
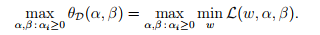对偶问题与原始问题的差别在于max和min的位置不同。同时定义
。
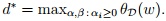通常情况下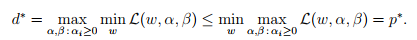
在某些特定的情况下，两者取同一值。所以可以使用对偶问题的求解代替原始问题的求解。
两者相等的条件是：令f是一个凸函数，h_i是一个仿射函数(有截距的线性函数)，g_i是严格可执行的(意味着存在一些w使得对于所有的i来说，g_i(w)<0成立)。
在这种情况下存在w*,alpha*,beta*。使得w*是原始问题的解，alpha*,beta*是对偶问题的解，同时p*=d*=L(lagrange算子)。并且w，alpha,beta还要满足KKT条件
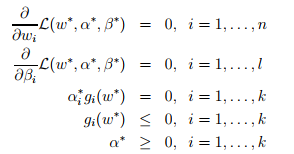如果，alpha*_i>0,那么就蕴含着g_i(w*)=0(此时的g_i(w*)是一个活动约束)。
继续最优边界分类器
求解最优边界时，即进行
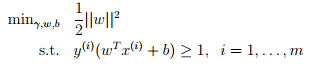令，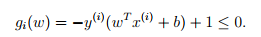
。如果，alpha_i>0，那么函数间隔就为1。函数间隔为1的点称为支持向量。对于最优边界的lagrange算子可以写成
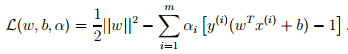。相应的对偶问题为
theta_D(alpha)=min_w,b L(w,b,alpha)。那么求出对偶问题的过程为
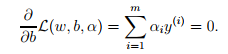
将结果带入lagrange算子中，可以得到
。此时对偶问题已经表示了出来，要进行对偶最优化求解，对偶最优化求解可以描述为
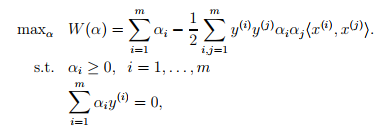
这是关于alpha的求解过程，求出了alpha后，根据可以求出w，求出alpha与w后，也可以求出b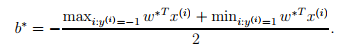
另外，我们要的预测函数为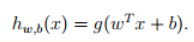
根据可以得到
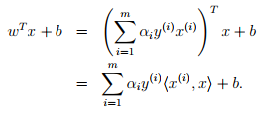有时候要使用到的样本维数会很高，有时甚至是无限维。使用kernel可以进行高维度样本内积的计算。