hdu 3038 How Many Answers Are Wrong (带权并查集)

• 题意: 长度为(n)的序列,给出(m)个问题,表示为a,b区间和为v,但有可能跟前面的冲突,计算冲突的数量(冲突后的问题不再更新序列)
• 思路: 带权并查集,权表示当前点到父亲的区间和,对于每个(a,b,v)都有:
  当a,b父亲不同:对齐进行合并
  
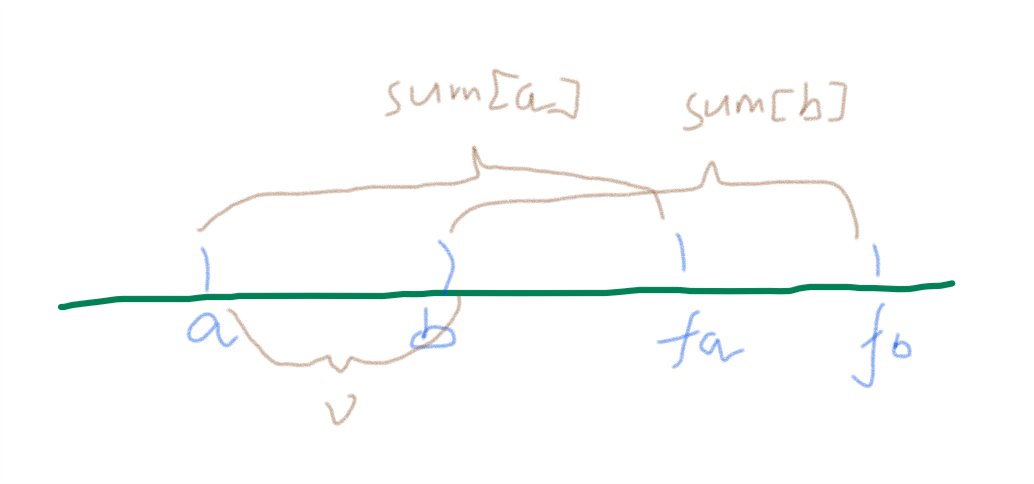
  对于a,b父亲相同时:判断是否合法
  

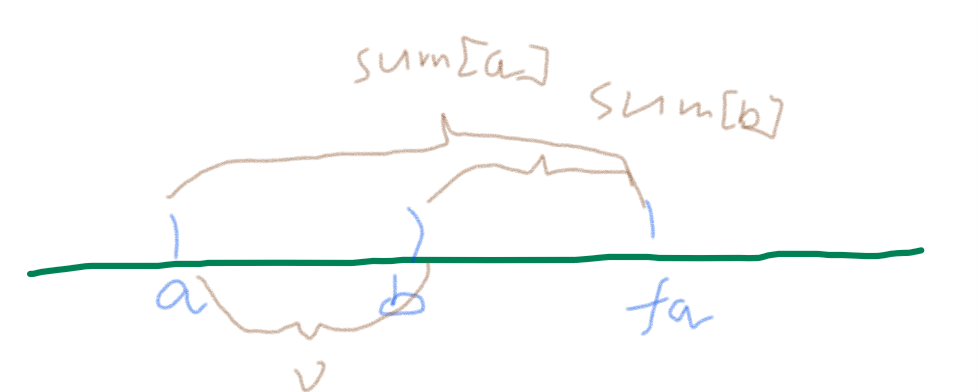
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <stdlib.h>
#include <vector>
#include <queue>
#include <cmath>
#include <stack>
#include <map>
#include <set>
#define ll long long
#define FOR(i,l,r) for(int i = l ; i <= r ;++i )
#define inf 1<<30
#define EPS (1e-9)
#define ALL(T)  T.begin(),T.end()
#define lson(i)     i<<1
#define rson(i)     (i<<1|1)
using namespace std;
typedef pair<int,int> pii;
const int maxn = 200010;
int fa[maxn];
int sum[maxn];

int find(int k){
    if(fa[k]==k)    return k;
    int f = fa[k];	// 路径压缩前的父亲
    fa[k] = find(fa[k]);
    sum[k] += sum[f];	// 更新距离(f点已经更新过了)
    return fa[k];
}

int main(){
    int n,m;
    while(cin >> n >> m){
        
    FOR(i,0,n){
        fa[i] = i;
        sum[i] = 0;
    }
    int l,r,v;
    int ans = 0;
    FOR(i,1,m){
        cin>> l >> r >> v;
        int fl = find(--l);
        int fr = find(r);
        if(fl==fr){	// 同一集合
            if(sum[l]-sum[r]!=v)    ans++;
        }else{	// 不同集合,合并
            fa[fl] = fr;
            sum[fl] = sum[r]-sum[l]+v;
        }
    }
    cout<< ans<< endl;
    }
    return 0;
}

注意: 题目所给的a,b区间是闭区间,为了能够合并,需要移动左端点(或右端点)使其成为左开右闭区间,才能进行区间合并.
显然((a,b]cup(b,c]=(a,c]),([a,b]cup[b,c]!=[a,c])

博客连接,大佬讲解的比较详细
题目连接