数论之卢卡斯定理

题目描述：

给定n,m,p(1<=n,m,p<=10^5)

求C^m_n+m %p

保证P为prime

C表示组合数。

题目链接：https://www.luogu.org/problemnew/show/P3807

卢卡斯定理，就是用来计算很大的组合数的。

具体如下：C(n, m) % p  =  C(n / p, m / p) * C(n%p, m%p) % p

证明如下：

首先证明 在模p意义下

  

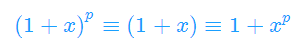
证明法一：

由费马小定理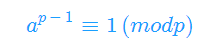， 得

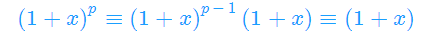
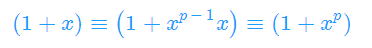
证明法二：

当j∈[1,p-1] 时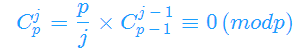， （p是质数，j∈[1,p-1]，j在模p意义下一定有逆元）

用二项式定理展开（1+x）^p

 

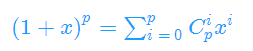
除了第一项和最后一项，中间项的组合数在模p意义下是0

所以

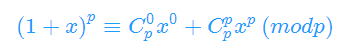
注意下图是在模P的前提下

b=n%p d=m%p

 

声明：以上证明过程来自某大佬的博客http://www.cnblogs.com/TheRoadToTheGold/p/7358327.html，感谢！！！

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<malloc.h>
#include<cstring>
#define ll long long
using namespace std;

const int maxn=1e5+15;

ll jie[maxn];
ll inline read()
{
    char ch=getchar();
    ll s=0;
    int f=1;
    while (!(ch>='0'&&ch<='9')) {if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9') {s=(s<<3)+(s<<1)+ch-'0';ch=getchar();}
    return s*f;
 }
void ins(ll a,ll p)
{
    jie[0]=1;
    for (int i=1;i<=a;i++) jie[i]=jie[i-1]*i%p;
}
ll pow(ll a,ll b,int p)
{
    ll ans=1;
    for (;b;b>>=1,a=a*a%p) if (b&1) ans=ans*a%p;
    return ans;
}
ll c(ll n,ll m,ll p)
{
    if (n<m) return 0;
    return jie[n]*pow(jie[n-m],p-2,p)%p*pow(jie[m],p-2,p)%p; 
}
ll C(ll n,ll m,ll p)
{
    if (n<m) return 0;
    if (!m) return 1;
    return (C(n/p,m/p,p)%p*c(n%p,m%p,p)%p)%p;
 }
int main()
{
    ll t;
    t=read();
    while (t--)
    {
        ll n,m,p;
        n=read();
        m=read();
        p=read();
        ins(m+n,p);
        printf("%lld
",C(n+m,m,p));
    }
    return 0;
}