[JZOJ 5909] [NOIP2018模拟10.16] 跑商（paoshang） 解题报告 （圆方树）

题目链接：

https://jzoj.net/senior/#contest/show/2529/2

题目：

题目背景：
尊者神高达很穷，所以他需要跑商来赚钱
题目描述：
基三的地图可以看做 n 个城市，m 条边的无向图，尊者神高达会从任意一个点出发并在起点购买货物，在旅途中任意一点卖出并最终到达终点，尊者神高达的时间很宝贵，所以他不会重复经过同一个城市，但是为了挣钱，他可能会去绕路。当然，由于工作室泛滥，所以一个城市的货物价格可能会发生改变。但是尊者神高达智商不足，他可能在一个很蠢的节点把货物卖掉，所以尊者神高达想知道每一次跑商最多能赔多少钱。

题目大意：

一张无向图，询问两点之间的可能的路径上的最小点权，带修改

前置知识点：

圆方树相关内容

---

 首先我们看圆方树

圆方树连边规则：

如果一条边在仙人掌中不属于任何一个环中，那么它直接圆方树中的两个圆点。

对于仙人掌中的任意一个环，则每个环上的点在圆方树上对应的圆点向这个环对应的方点连边。如下图所示

注意圆方树只适用于仙人掌

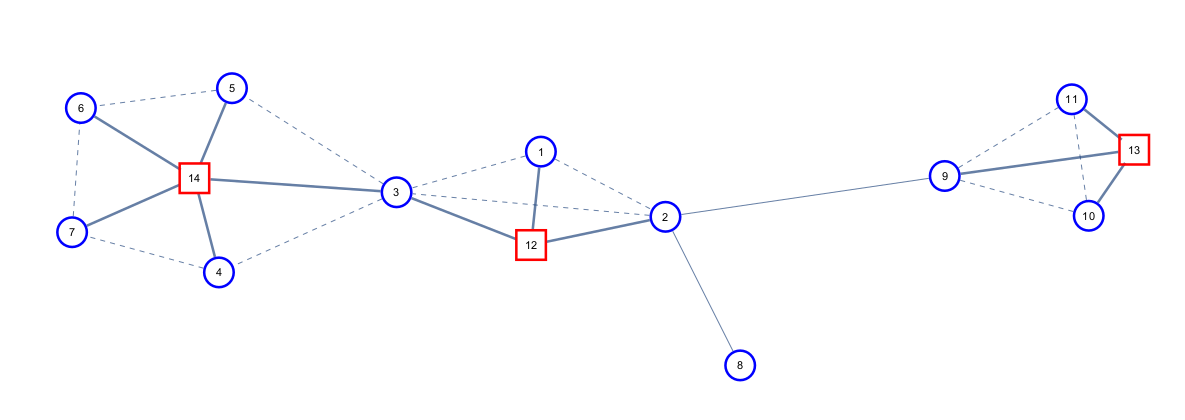
 怎么构造圆方树呢？

代码实现大概是这样的

void tarjan(int x,int pre)
{
    dfn[x]=low[x]=++js;sta[++tp]=x;
    for (int i=h1[x];i;i=e1[i].nxt)
    {
        if (i==(pre^1)) continue;
        int y=e1[i].to;
        if (!dfn[y])
        {
            tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if (low[y]>dfn[x]) link2(x,y),tp--;//找到桥 
            if (low[y]==dfn[x])//x在边双里 
            {
                for (++nn,link2(x,nn);sta[tp]!=x;tp--) A[nn].insert(a[sta[tp]]),link2(nn,sta[tp]);
            }
        }
        else low[x]=min(low[x],dfn[y]);
    }
}

---

那么广义圆方树呢？

构造方法和圆方树区别不大，就是强制把两点一线也看成一个点双，建方点即可。

广义圆方树可以适用于无向图，而不只是仙人掌

---

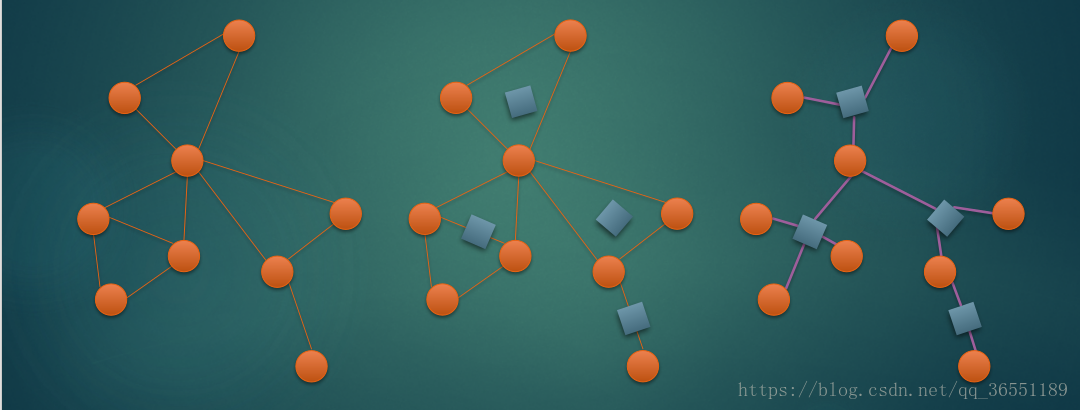
题解：

言归正传，这道题我们怎么做？

如果没有修改的话，很显然，每个方点的值为这个点双中权值最小的点。 这样，就变成了裸的求树上两点路径上最小值，剖一下就行了

考虑这样怎么修改，记录下每一个圆点连接的方点，开个set维护一下每个方点连接的原点。对于修改的原点一个个修改每个与它相连的方点，但如果这个点是一个割点（连接很多个方点），那么可能就需要修改很多次，时间复杂度就不对了

题解用了更优秀的做法

把圆方树变成一个有根树，方点的值改为记录环上除环的根外权值最小的点，这样每个圆点只有一个对应的方点。如果 LCA 是方点，只需特判一下LCA的父亲。画个图理解吧

然而代码里写的广义圆方树用的是圆方树的构造方法，身为蒟蒻的我不知道两种构造方法有什么区别...这是我第一次写圆方树

还有与圆方树类似的做法，就是对每一个边双维护一个set，每次修改就是修改这个点所在的边双即可

注意边双和点双都意味着其中的任意两个点可以经过任意一个想经过的点到达彼此

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<set>
using namespace std;

const int N=2e5+15;
const int inf=1e9;
int n,m,tot1=1,tot2=1,js,tp,nn;
int a[N],h1[N],h2[N],dfn[N],low[N],sta[N],siz[N],dd[N],id[N],dep[N],son[N],top[N],pf[N];
int mi[N<<2];
multiset <int> A[N];
struct EDGE
{
    int to,nxt;
}e1[N<<1],e2[N<<1];
inline int read()
{
    char ch=getchar();
    int s=0,f=1;
    while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
    while (ch>='0'&&ch<='9') {s=(s<<3)+(s<<1)+ch-'0';ch=getchar();}
    return s*f;
}
void link1(int u,int v)
{    
    e1[++tot1]=(EDGE){v,h1[u]};
    h1[u]=tot1;
}
void link2(int u,int v)
{    
    pf[v]=u;
    e2[++tot2]=(EDGE){v,h2[u]};
    h2[u]=tot2;
}
void tarjan(int x,int pre)//构造园方树 
{
    dfn[x]=low[x]=++js;sta[++tp]=x;
    for (int i=h1[x];i;i=e1[i].nxt)
    {
        if (i==(pre^1)) continue;
        int y=e1[i].to;
        if (!dfn[y])
        {
            tarjan(y,i);
            low[x]=min(low[x],low[y]);
            if (low[y]>dfn[x]) link2(x,y),tp--;//找到桥 
            if (low[y]==dfn[x])//x在点双里 
            {
                for (++nn,link2(x,nn);sta[tp]!=x;tp--) A[nn].insert(a[sta[tp]]),link2(nn,sta[tp]);
            }
        }
        else low[x]=min(low[x],dfn[y]);
    }
}
void dfs1(int x)
{
    siz[x]=1;
    for (int i=h2[x];i;i=e2[i].nxt)
    {
        int y=e2[i].to;
        if (y==pf[x]) continue;
        dep[y]=dep[x]+1;
        dfs1(y);
        siz[x]+=siz[y];
        if (!son[x]||siz[y]>siz[son[x]]) son[x]=y;
    }
}
void dfs2(int x,int tt)
{
    dd[x]=++js;id[js]=x;
    top[x]=tt;
    if (!son[x]) return;
    dfs2(son[x],tt);
    for (int i=h2[x];i;i=e2[i].nxt)
    {
        int y=e2[i].to;
        if (y==pf[x]||y==son[x]) continue;
        dfs2(y,y);
    }
}
#define mid ((l+r)>>1)
void pushup(int o) {mi[o]=min(mi[o<<1],mi[o<<1|1]);}
void build(int o,int l,int r)
{
    if (l==r) {mi[o]=a[id[l]];return;}
    build(o<<1,l,mid);build(o<<1|1,mid+1,r);
    pushup(o);
}
void update(int o,int l,int r,int x,int y)
{
    if (l==r) {mi[o]=y;return;}
    if (x<=mid) update(o<<1,l,mid,x,y);
    else update(o<<1|1,mid+1,r,x,y);
    pushup(o);
}
int query(int o,int l,int r,int x,int y)
{
    if (l>=x&&r<=y) return mi[o];
    int re=inf;
    if (x<=mid) re=min(re,query(o<<1,l,mid,x,y));
    if (y>mid) re=min(re,query(o<<1|1,mid+1,r,x,y));
    return re; 
}
int query_min(int x,int y)
{
    int re=inf;
    while (top[x]!=top[y])
    {
        if (dep[top[x]]<dep[top[y]]) swap(x,y);
        re=min(re,query(1,1,nn,dd[top[x]],dd[x]));
        x=pf[top[x]];
    }
    if (dep[x]<dep[y]) swap(x,y);
    re=min(re,query(1,1,nn,dd[y],dd[x]));
    if (y>n&&pf[y]) re=min(re,a[pf[y]]);//特判LCA是否是方点，如果是的话还需要考虑它的父亲 
    return re;
}
int main()
{
    freopen("paoshang.in","r",stdin);
    freopen("paoshang.out","w",stdout);
    n=read();m=read();nn=n;
    for (int i=1;i<=n;i++) a[i]=read();
    for (int i=1,u,v;i<=m;i++)
    {
        u=read();v=read();
        link1(u,v);link1(v,u);
    } 
    js=0;tarjan(1,-1);
    for (int i=n+1;i<=nn;i++) a[i]=*A[i].begin();
    dep[1]=1;dfs1(1);
    js=0;dfs2(1,1);
    build(1,1,nn);
    int q=read(),pr,pl;
    char op[5];
    while (q--)
    {
        scanf("%s",op);
        if (op[0]=='C')
        {
            int x=read(),y=read();
            update(1,1,nn,dd[x],y);
            if ((pr=pf[x])>n)
            {
                A[pr].erase(A[pr].find(a[x]));A[pr].insert(y);
                if (a[pr]!=(pl=*A[pr].begin())) update(1,1,nn,dd[pr],pl),a[pr]=pl;
             }
             a[x]=y;
        }
        if (op[0]=='Q')
        {
            int x=read(),y=read();
            printf("%d
",a[x]-query_min(x,y));
        }
    }
    return 0;
}