原文链接:https://blog.csdn.net/zengxiantao1994/article/details/72787849
贝叶斯决策
贝叶斯分类
贝叶斯公式:$$p(w|x)=frac{p(x|w)p(w)}{p(x)}$$
其中:p(w):为先验概率,表示每种类别分布的概率;(p(x|w))为类条件概率,表示在某种类别前提下,某事发生的概率;(p(w|x))为后验概率,表示某事发生了,并且它属于某一类别的概率,有了这个后验概率,我们就可以对样本进行分类。后验概率越大,说明某事物属于这个类别的可能性越大,我们越有理由把它归到这个类别下。

在实际问题中,我们能获得的数据可能只有有限数目的样本数据,而先验概率(p(w_i))和类条件概率(各类的总体分布)(p(x|w_i))都是未知的。根据仅有的样本数据进行分类时,一种可行的办法是我们需要先对先验概率和类条件概率进行估计,然后再套用贝叶斯分类器。
先验概率的估计较简单,1、每个样本所属的自然状态都是已知的(有监督学习);2、依靠经验;3、用训练样本中各类出现的频率估计。
类条件概率的估计(非常难),原因包括:概率密度函数包含了一个随机变量的全部信息;样本数据可能不多;特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是,把估计完全未知的概率密度(p(x|w_i))转化为估计参数。这里就将概率密度估计问题转化为参数估计问题,极大似然估计就是一种参数估计方法。
由于参数估计问题只是实际问题求解过程中的一种简化方法(由于直接估计类条件概率密度函数很困难)。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。
重要前提:训练样本的分布能代表样本的真实分布。每个样本集中的样本都是所谓独立同分布的随机变量,且有充分的训练样本。
极大似然估计
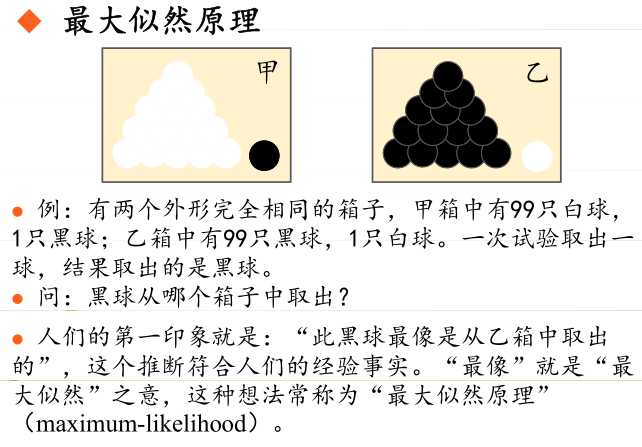
最大似然估计的目的就是:利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
原理:极大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
由于样本集中的样本都是独立同分布,可以只考虑一类样本集(D),来估计参数向量( heta)。记已知的样本集为:(D={x_1,x_2,cdots , x_N})
似然函数:联合概率密度函数(p(D| heta))称为相对于({x_1,x_2,cdots , x_N})的( heta)的似然函数:(l( heta)=p(D| heta)=p(x_1,x_2,cdots,x_N| heta)=displaystyle prod^N_{i=1}p(x_i| heta))
如果(hat{ heta})是参数空间中能使似然函数(l( heta))最大的( heta)值,则(hat{ heta})就是θ的极大似然估计量。它是样本集的函数,记作:(hat{ heta}=d(x_1,x_2,cdots,x_N)=d(D))
求解极大似然函数
ML估计:求使得出现该组样本的概率最大的θ值。$$hat{ heta}=arg underset{ heta}max l( heta)=arg underset{ heta}max displaystyle prod^N_{i=1}p(x_i| heta)$$
定义对数似然函数:(H( heta)=ln l( heta))
替换为:$$hat{ heta}=arg underset{ heta}max H( heta)=arg underset{ heta}max ln l( heta)=arg underset{ heta}max displaystyle prod^N_{i=1}ln p(x_i| heta)$$
可以看出:1. 未知参数只有一个(θ为标量)。在似然函数满足连续、可微的正则条件下,极大似然估计量是下面微分方程的解:(frac{dl( heta)}{d heta}=0)或者等价于(frac{dH( heta)}{d heta}=frac{d lnl( heta)}{d heta}=0)
2.未知参数有多个(θ为向量),则θ可表示为具有S个分量的未知向量:( heta=[ heta_1, heta_2,cdots, heta_S]^T)
记梯度算子:(
abla_ heta=[frac{partial}{partial heta_1},frac{partial}{partial heta_2},cdots,frac{partial}{partial heta_S}]^T)
若似然函数满足连续可导的条件,则最大似然估计量就是如下方程的解:(
abla_ heta H( heta)=
abla_ heta lnl( heta)=sum_{i=1}^N
abla_ heta lnP(x_i| heta)=0)
P.S.方程的解只是一个估计值,只有在样本数趋于无限多的时候,它才会接近于真实值。