Q:给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
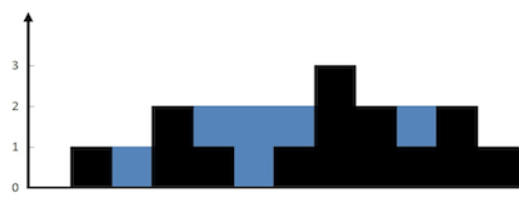
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
A:
(引用自《labuladong的算法小抄》)
位置 i 能达到的⽔柱⾼度和其左边的最⾼柱⼦、右边的最⾼柱⼦有关,我们分别称这两个柱⼦⾼度为 l_max和 r_max ;位置 i 最⼤的⽔柱⾼度就是 min(l_max, r_max) 。
用一个备忘录记录一下:
public int trap(int[] height) {
if (height.length <= 2)
return 0;
int n = height.length;
int[] l_max = new int[n];
l_max[0] = height[0];
int[] r_max = new int[n];
r_max[n - 1] = height[n - 1];
//左侧最高
for (int i = 1; i < n; i++) {
l_max[i] = Math.max(l_max[i - 1], height[i]);
}
//右侧最高
for (int i = n - 2; i >= 0; i--) {
r_max[i] = Math.max(r_max[i + 1], height[i]);
}
int sum = 0;
for (int i = 1; i < n - 1; i++) {
sum += Math.min(l_max[i], r_max[i]) - height[i];
}
return sum;
}
使用双指针法:
public int trap(int[] height) {
if (height.length <= 2)
return 0;
int n = height.length;
int left = 0, right = n - 1;
int l_max = height[0], r_max = height[n - 1];
int sum = 0;
while (left <= right) {
l_max = Math.max(l_max, height[left]);
r_max = Math.max(r_max, height[right]);
if (l_max > r_max) {
sum += r_max - height[right];
right--;
} else {
sum += l_max - height[left];
left++;
}
}
return sum;
}
很容易理解, l_max 是 height[0..left] 中最⾼柱⼦的⾼度, r_max 是 height[right..end] 的最⾼柱⼦的⾼度。此时的 l_max 是 left 指针左边的最⾼柱⼦,但是 r_max 并不⼀定是left 指针右边最⾼的柱⼦,这真的可以得到正确答案吗?
其实这个问题要这么思考,我们只在乎 min(l_max, r_max) 。对于上图的情况,我们已经知道 l_max < r_max 了,⾄于这个 r_max 是不是右边最⼤的,不重要,重要的是 height[i] 能够装的⽔只和 l_max 有关。

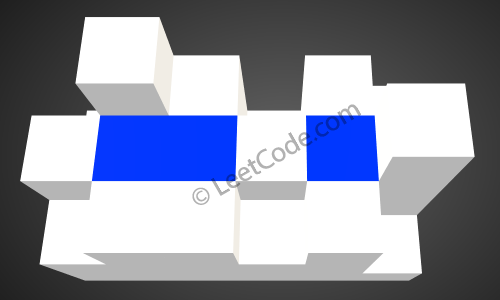
Q:给你一个 m x n 的矩阵,其中的值均为正整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
示例:
给出如下 3x6 的高度图:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
返回 4 。

A:引用:https://blog.csdn.net/qq_29996285/article/details/86696301
思路:
- 搜索队列使用优先级队列(STL的优先队列的底层实现默认是大顶堆),越低的点优先级越高(构造小顶堆),优先级越高的点越优先搜索。
- 以矩阵四周的点作为起始点进行广度优先搜索(这些点在搜索前需要push进队列中)。
- 使用一个二维数组对push进队列的点进行标记,如果该点被标记过,则不会被push到队列中。
- 只要优先级队列不空,即去除优先级队列的队头元素进行搜索,按照上下左右四个方向进行扩展,扩展过程中忽略超出边界的点和已经入队的点。
- 当某个点 (x, y, h) 进行拓展时,得到的新点 (newx, newy) 的高度 height 小于 h,则——积水高度+=h-height;,并更新 h 的值为 height 。
- 将(newx, newy, height)入队,并做上标记。
举例:

将四周的点添加至优先队列Q中,并做上标记
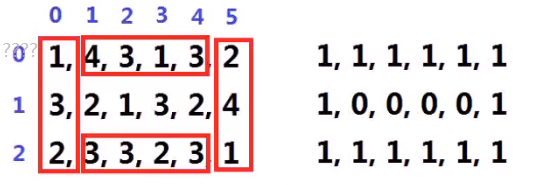
开始进行扩展:
蓝色代表正在搜索的节点,绿色代表队中的节点,紫色代表已完成节点,红色代表扩展的新节点(优先级队列中的元素:优先队列<行,列,高>)


代码:
public int trapRainWater(int[][] heightMap) {
if (heightMap.length <= 2 || heightMap[0].length <= 2)
return 0;
int n = heightMap.length;
int m = heightMap[0].length;
boolean[][] visit = new boolean[n][m];
PriorityQueue<int[]> pq = new PriorityQueue<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (i == 0 || i == n - 1 || j == 0 || j == m - 1) {
pq.offer(new int[]{i, j, heightMap[i][j]});
visit[i][j] = true;
}
}
}
int res = 0;
int[] dirs = {-1, 0, 1, 0, -1};
while (!pq.isEmpty()) {
//小跟堆的最小高度
int[] poll = pq.poll();
for (int k = 0; k < 4; k++) {
int newx = poll[0] + dirs[k];
int newy = poll[1] + dirs[k + 1];
if (newx >= 0 && newy >= 0 && newx < n && newy < m && !visit[newx][newy]) {
//比当前这个最小高度还小,说明里面可以装水
if (poll[2] > heightMap[newx][newy])
res += (poll[2] - heightMap[newx][newy]);
//放入堆
pq.offer(new int[]{newx, newy, Math.max(heightMap[newx][newy], poll[2])});
visit[newx][newy] = true;
}
}
}
return res;
}