题目描述
下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由(1)(->)(n)。试用动态规划的最优化原理求出(1)(->)(n)的最省费用
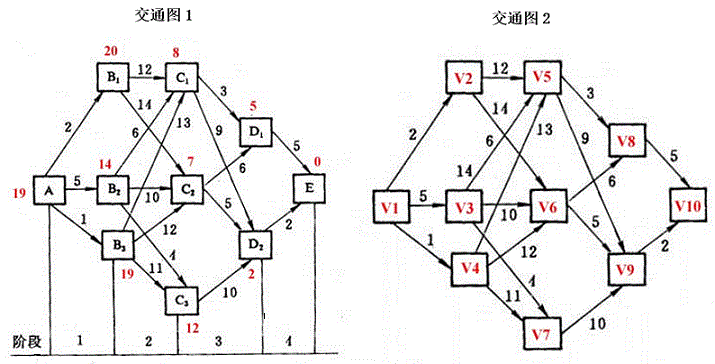
(左图没有任何用处)
如图:求v1到v10的最短路径长度及最短路径。
输入
第一行为城市的数量N;
后面是N*N的表示两个城市间费用组成的矩阵。
输出
(1)(->)(n)的最省费用
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=100+5;
int n,a[maxn][maxn],ans,s[maxn],path[maxn];//a[i][j]记录从i到j的距离,s[i]记录到点i是的最省费用,path[i]记录路径
inline void dfs(int i,int sum){//i是到了第i点,sum是当前的最省费用
if(i==n){
ans=min(ans,sum);
return ;
}//如果到了点n,就取最省费用
for(int j=i+1;j<=n;j++)//知道到编号比i大的点
if(a[i][j]){
if(sum+a[i][j]<s[j]){//如果到j点时的费用比原本费用大,就不用往下dfs
s[j]=sum+a[i][j];
path[j]=i;//记录路径
dfs(j,s[j]);
}
}
}
inline void out(int i){//倒序输出
if(i==1){
printf("%d",i);
return ;
}
out(path[i]);
printf(" %d",i);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
cin>>a[i][j];//输入
ans=1e9;//因为取最小值,所以ans定最大
for(int i=1;i<=n;i++)
s[i]=1e9;//同ans
dfs(1,0);
printf("minlong=%d
",ans);
out(n);//输出
return 0;
}