并不对劲的st表

对于带修改的区间求和能做到O(n log n)预处理，O(log n)查询；而不带修改的可以做到O(n)预处理，O(1)查询。那么不带修改的区间最值能做到O(1)查询吗？

区间最值有这样一个性质：对于一段区间的两个子区间，如果它们覆盖了整个区间（可以有重叠部分），那么这两段区间各自的最大（或最小）值的最大（或最小）值就等于整个区间的最大（或最小）值。

这样的话，可以倍增地求出从每个位置开始的2的x次方的区间最值，预处理每个数的log。查询l-r这一段区间时按如图所示的方式合并就行了。

 

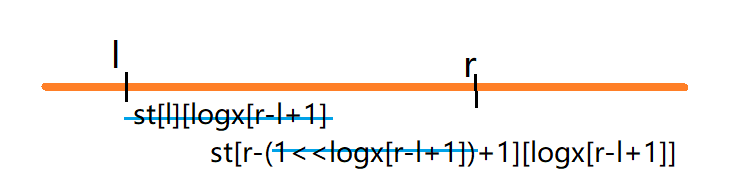
#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#define maxn 100010 
using namespace std;
int read()
{
	int f=1,x=0;char ch=getchar();
	while(isdigit(ch)==0 && ch!='-')ch=getchar();
	if(ch=='-')f=-1,ch=getchar();
	while(isdigit(ch))x=x*10+ch-'0',ch=getchar();
	return x*f;
}
void write(int x)
{
	int ff=0;char ch[15];
	if(x<0)
	{
		x=-x;
		putchar('-');
	}
	while(x)ch[++ff]=(x%10)+'0',x/=10;
	if(ff==0)putchar('0');
	while(ff)putchar(ch[ff--]);
	putchar('
');
}
struct ST
{
	int st[maxn][20],logx[maxn],two[maxn];
	int n,q,l,r;
	void ask()
	{
		l=read(),r=read();
		write(max(st[l][logx[r-l+1]],st[r-two[r-l+1]+1][logx[r-l+1]]));
	}
	void work()
	{
		n=read(),q=read();
		for(int i=1,j=1,k=0;i<=n;i++)
	    {
	    	st[i][0]=read();
			if((j<<1)<=i)j<<=1,k++;
			logx[i]=k;
			two[i]=j;
		} 
		for(int i=1;(1<<i)<=n;i++)
		{
			for(int j=1;j+(1<<(i))-1<=n;j++)
			{
				st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);
			//	cout<<st[j][i]<<" "; 
			}//cout<<endl;
		}
		while(q--)
		{
			ask();
		}
	}//1 2 3 4 5
}t;
int main()
{
	t.work();
	return 0;
}/*
8 8
9 3 1 7 5 6 0 8
1 6
1 5
2 7
2 6
1 8
4 8
3 7
1 8
*/