据说这些并不对劲的内容是《信息学奥赛一本通提高篇》的配套练习。
先感叹一句《信息学奥赛一本通提高篇》上对kmp的解释和matrix67的博客相似度99%(还抄错了),莫非matrix67藏在编者之中?
但这不重要,因为并不对劲的人不会对kmp作出任何解释。
课后练习:
可以将题目中给出的字符串看成形如这样的串:

那么,对于其中的某一位:

它到当前前缀的第二个循环节的开始组成的子串和前缀相等:
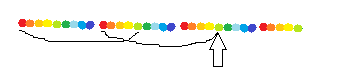
所以,对于当前位置x,fail[x]就是它到当前前缀的第二个循环节的开始组成的子串的长度,x-fail[x]就相当于字符串的开始到当前前缀的第二个循环节的开始的长度,也就是一个循环节的长度:
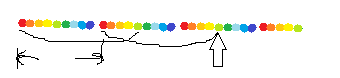
但是,随着x增大,x-fail[x]不降,所以对于长度为n的串,答案就是n-fail[n]。

代码就是求fail指针就行了。
#include<bits/stdc++.h>
using namespace std;
#define maxn 1000010
int fa[maxn],n,ans;
char s[maxn];
int main()
{
scanf("%d%s",&n,s+1);
fa[0]=-1,fa[1]=0;ans=1;
for(int i=2;i<=n;i++)
{
int u=i-1;
while(u&&s[fa[u]+1]!=s[i])u=fa[u];
if(u)fa[i]=fa[u]+1;
else fa[i]=0;
}
printf("%d",n-fa[n]);
return 0;
}
并不能读懂题面,求大佬帮助。
题目中要找形如A+B+A的子串,所以可以枚举左端点,再算出每个右端点是否可行。
首先,固定左端点后,求出fail指针。对于fail[x]*2<x的,肯定是没问题了(如图):

对于fail[x]*2>=x的呢?会发现,1到fail[x]的子串和x-fail[x]+1到x的子串一样,1到fail[fail[x]]的子串和fail[x]-fail[fail[x]]+1到fail[x]的子串一样,所以1到fail[fail[x]]的子串和x-fail[fail[x]]+1到x的子串一样。那么就可以顺着fail指针往上找,直到长度*2<x且长度>=k。
不断顺着fail指针往上找的过程听上去很暴力,这题本来就很暴力了,就要避免这种暴力的。发现对于点x求出合法解为y后,对于x在fail树所有子孙,就都是合法的了。那么可以标记x,这样计算x在fail树所有子孙时,走到x就可以停了。
这个优化听上去很扯,它还是O(n2)的,但是15000的数据还是过了,是因为kmp常数小的缘故?
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<stack>
#include<set>
#include<queue>
#define maxn 15010
using namespace std;
int read()
{
int x=0,f=1;
char ch=getchar();
while(!isdigit(ch)&&ch!='-')ch=getchar();
if(ch=='-')f=-1,ch=getchar();
while(isdigit(ch))x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
return x*f;
}
void write(int x)
{
int f=0;char ch[20];
if(x==0){putchar('0'),putchar('
');return;}
if(x<0){putchar('-'),x=-x;}
while(x)ch[++f]=x%10+'0',x/=10;
while(f)putchar(ch[f--]);
putchar('
');
}
int ans,k,fa[maxn],n,lst[maxn];
char s[maxn];
void rebuild()
{
for(int i=1;i<n;i++)s[i]=s[i+1];
n--;
}
int main()
{
scanf("%s%d",s+1,&k);
n=strlen(s+1);
for(;n>=(k<<1|1);)
{
fa[1]=0,fa[0]=-1;lst[0]=lst[1]=-1;
for(int i=2;i<=n;i++)
{
lst[i]=-1;
int u=i-1;
while(s[fa[u]+1]!=s[i]&&u)u=fa[u];
if(!u)fa[i]=0;
else fa[i]=fa[u]+1;
}
for(int i=1;i<=n;i++)
{
int u=fa[i];
while((u<<1|1)>i&&fa[u]>=k){if(lst[u]!=-1)u=lst[u];else u=fa[u];}
//cout<<u<<endl;
if((u<<1|1)<=i&&u>=k) lst[i]=u,ans++;
//cout<<lst[i]<<" ";
}
//cout<<"+++"<<endl;
rebuild();
}
write(ans);
return 0;
}
/*
aaaaa
1
*/
先想一个比较暴力的:让一个指针k从头往后扫S,每次判断长度为|T|的后缀是否等于T。
这个的时间复杂度是O(|S|*|T|),发现判断长度为|T|的后缀是否等于T有点像kmp。
那么就可以再维护一个指针p,表示T中走到的位置。对于S的每一位,开一个数组记录k走到这里时p走到的位置。
每当p走到T的结尾时,k退回|T|前的位置,p变成之前记录的k走到该点时p的位置。
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<set>
#include<stack>
#include<queue>
#define maxn 1000010
using namespace std;
char s[maxn],t[maxn];
int fa[maxn],mat[maxn],top,ns,nt,ans[maxn];
void go(int & u,char c)
{
while(t[u+1]!=c){u=fa[u];if(!u)break;}
if(t[u+1]==c)u++;
else u=0;
}
int main()
{
//freopen("censor.in","r",stdin);
//freopen("censor.out","w",stdout);
scanf("%s%s",s+1,t+1);
ns=strlen(s+1),nt=strlen(t+1);
fa[1]=0;
for(int i=2;i<=nt;i++)
{
int u=i-1;
while(t[fa[u]+1]!=t[i]&&u)u=fa[u];
if(!u)fa[i]=0;
else fa[i]=fa[u]+1;
}
int u=0;
for(int i=1;i<=ns;i++)
{
go(u,s[i]);
mat[i]=u;
ans[++top]=i;
if(u==nt)
{
top-=nt;
u=mat[ans[top]];
}
}
//for(int i=1;i<=ns;i++)cout<<mat[i]<<" ";cout<<endl;
for(int i=1;i<=top;i++)putchar(s[ans[i]]);
return 0;
}