并不对劲的素质四连（二）

为什么连续两天都中奖上去讲题？

d2t1

题意：后缀数组/哈希板子题

做法：后缀数组/哈希

d2t2

题意：T组数据，给n条线段，判断它们是否和某条线段有公共点，n<=10^4，T<=10，保证线段不是一个点

做法：可以先画这样一个图：

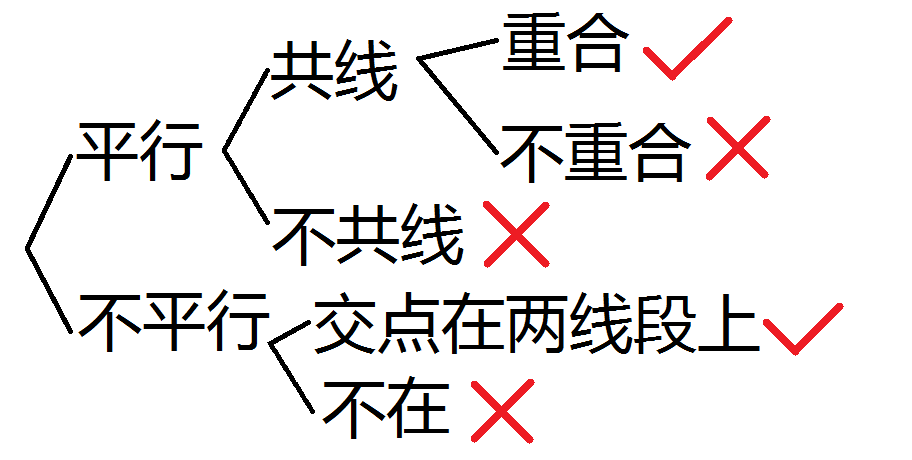
那么接下来就是要判断是否平行/共线/重合/交点在两线段上，设两线段为l₁和l₂，l₁的两端点为A₁和B₁，l₂的两端点为A₂和B₂：

1.判断平行：

为了防止用小数存导致精度问题，可以把它们的斜率写成分数形式，设为a₁/b₁和a₂/b₂。会发现b₁和b₂可能为0，特判会很麻烦，而且分数还得化简。所以要交叉相乘，把式子变成判断a₁*b₂和a₂*b₁是否相等

2.在平行的条件下判断共线：

在l₁上任取两点（或一点），在l₂上任取一点（或两点），保证三点不重合，当且仅当l₁和l₂共线时，以它们三个组成的三角形面积为0。那么就可以直接判断l₁的两端点和l₂的一个端点围成的三角形面积是否为0

3.在共线的条件下判断重合：

当且仅当两条线段重合时，存在一个端点在另一条线段上。那么就可以判断四个端点是否在另一条线段上

3.判断不平行的两线段的交点是否都在两线段上：

如果A、B在直线l两侧，那么l和l的交点在AB上，对于A和B和l也同理。那么就可以用叉积求出有向面积，通过正负判断两点是否在一条直线两侧。

#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<stack>
#include<set>
#include<queue>
#include<vector>
#define LL long long
using namespace std;
LL read()
{
	LL x=0,f=1;char ch=getchar();
	while(!isdigit(ch)&&ch!='-')ch=getchar();
	if(ch=='-')f=-1,ch=getchar();
	while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
	return x*f;
}
void write(LL x)
{
	LL f=0;char ch[20];
	if(x==0){putchar('0'),putchar('
');return;}
	if(x<0){putchar('-'),x=-x;}
	while(x)ch[++f]=x%10+'0',x/=10;
	while(f)putchar(ch[f--]);
	putchar('
');
}
typedef struct vect{LL x,y;}V;
typedef struct poin{LL x,y;}P;
typedef struct line{V v;P s,t;}L;
LL yesv(V x,V y){if((x.x==0&&x.y==0)||(y.x==0&&x.x==0))return 0;return (x.x==y.x&&x.y==y.y)?0:1;}
V make_v(LL x,LL y){V tmp;tmp.x=x,tmp.y=y;return tmp;}
P make_p(LL x,LL y){P tmp;tmp.x=x,tmp.y=y;return tmp;}
L make_l(V v,P s,P t){L tmp;tmp.v=v,tmp.s=s,tmp.t=t;return tmp;}
LL onl(P x,L y)
{
	LL maxx=max(y.s.x,y.t.x),maxy=max(y.s.y,y.t.y),minx=min(y.s.x,y.t.x),miny=min(y.s.y,y.t.y);
	if(x.x>=minx&&x.x<=maxx&&x.y>=miny&&x.y<=maxy)return 1;
	else return 0;
}
LL cros(P a,P b){return a.x*b.y-a.y*b.x;}
LL onv(L x,L y)
{
	if(!yesv(x.v,y.v)&&(cros(x.s,y.s)+cros(y.s,x.t)+cros(x.t,x.s)==0)&&(onl(x.s,y)||onl(x.t,y)||onl(y.s,x)||onl(y.t,x)))return 1;
	return 0;
}
LL sides(L x,L y)
{
	LL s1=cros(x.s,y.s)+cros(y.s,x.t)+cros(x.t,x.s),s2=cros(x.t,y.t)+cros(y.t,x.s)+cros(x.s,x.t);
	if(s1==0||s2==0)return 1;
	LL f=(((s1<0)^(s2<0))==0);
	if(f)return 1;
	return 0;
}
LL yesl(L a,L b)
{
	if(onv(a,b)){return 1;}
	if(!yesv(a.v,b.v)){return 0;}
	if(sides(a,b)&&sides(b,a)){return  1;}
	return 0;
}
LL n,T;
L a;
LL gcd(LL x,LL y)
{
	if(x>y)swap(x,y);
	if(x==0)return y;
	return gcd(y%x,x);
}
int main()
{
	freopen("intersect.in","r",stdin);
	freopen("intersect.out","w",stdout);
	T=read();
	while(T--)
	{
		n=read();
		LL xs=read(),ys=read(),xt=read(),yt=read();
		LL lx=xt-xs,ly=yt-ys,fx=(lx<0)?-1:1,fy=(ly<0)?-1:1;
		LL gdc=gcd(abs(lx),abs(ly));
		a=make_l(make_v(abs(lx)/gdc*fx,abs(ly)/gdc*fy),make_p(xs,ys),make_p(xt,yt));
		LL f=0;
		for(LL i=1;i<=n;i++)
		{
			LL xss=read(),yss=read(),xtt=read(),ytt=read();
			if(f)continue;
			LL lxx=xtt-xss,lyy=ytt-yss,fxx=(lxx<0)?-1:1,fyy=(lyy<0)?-1:1;
			LL gdcc=gcd(abs(lxx),abs(lyy));
			L b=make_l(make_v(abs(lxx)/gdcc*fxx,abs(lyy)/gdcc*fyy),make_p(xss,yss),make_p(xtt,ytt));
			if(!f)f|=yesl(a,b);
		}
		if(f)puts("YES");
		else puts("NO");
	}
	return 0;
}
/*
3
1
1 1 4 4
2 2 3 3
1
1 1 4 4
2 2 3 1
1
1 1 4 4
5 5 6 6
*/
/*
3
1
2 1 4 1
5 1 4 2
1
3 2 1 4
3 3 2 4
1
5 1 4 2
4 2 3 3
*/

　　

d2t3

题意：有一个n个点，m条无向边的图，每条边有两个系数，c和w，表示经过该边要花c的能量，只有当能量大于等于w时才能够走这条边。问从1号点出发，至少携带多少能量才能走到n，n,m<=10^5，1<=c<=10^3，1<=w<=10^9

做法：dis[i]表示从编号为i的点出发，走到n最少需要多少能量。转移是dis[u]=min{max(w[k],dis[v[k]]+c[k])}。然而并不对劲的人dijkstra忘记改大根堆，非常难受。

#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iomanip>
#include<iostream>
#include<map>
#include<stack>
#include<set>
#include<queue>
#include<vector>
#define maxn 100010
#define maxm 200010
#define pii pair<int ,int>
#define fi first
#define se second
using namespace std;
int read()
{
	int x=0,f=1;char ch=getchar();
	while(!isdigit(ch)&&ch!='-')ch=getchar();
	if(ch=='-')f=-1,ch=getchar();
	while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
	return x*f;
}
void write(int x)
{
	int f=0;char ch[20];
	if(x==0){putchar('0'),putchar('
');return;}
	if(x<0){putchar('-'),x=-x;}
	while(x)ch[++f]=x%10+'0',x/=10;
	while(f)putchar(ch[f--]);
	putchar('
');
}
priority_queue<pii>q;
int dis[maxn],fir[maxn],nxt[maxm],v[maxm],c[maxm],w[maxm],vis[maxn],cnt,n,m;
void ade(int u1,int v1,int c1,int w1){v[cnt]=v1,w[cnt]=w1,c[cnt]=c1,nxt[cnt]=fir[u1],fir[u1]=cnt++;}
int main()
{
	freopen("spaceship2.in","r",stdin);
	freopen("spaceship2.out","w",stdout);
	memset(dis,0x7f,sizeof(dis));
	memset(fir,-1,sizeof(fir));
	n=read(),m=read();
	for(int i=1;i<=m;i++)
	{
		int a=read(),b=read(),c=read(),d=read();
		ade(a,b,c,d),ade(b,a,c,d);
	}
	dis[n]=0;q.push(make_pair(0,n));
	while(!q.empty())
	{
		int u=q.top().se;q.pop();
		if(vis[u])continue;vis[u]=1;
		for(int k=fir[u];k!=-1;k=nxt[k])
		{
			int now=max(w[k],c[k]+dis[u]);
			if(dis[v[k]]>now)
			{
				dis[v[k]]=now;
				q.push(make_pair(-now,v[k]));
			}
		}
	}
	if(dis[1]==dis[0])write(-1);
	else write(dis[1]);
	return 0;
}
/*
4 4
1 2 1 1
2 3 1 10
2 3 5 6
3 4 1 1
*/
/*
4 4
1 2 1 1
2 3 1 1
2 3 5 6
3 4 1 1
*/
/*
4 2
1 2 1 3
2 3 1 4
*/